2018 西安交通大学数学建模竞赛

全文共: 6.3k字   |   阅读时长: 26分
知识整理本科课程大一
  阅读

文章导航

大一下数学建模校内赛论文（二等奖存档）

陆基导弹打击航母的数学建模问题

摘要

本文主要研究陆基反舰导弹打击航母的动态轨道问题。为了精确快速打击敌方航母，同时避免导弹被敌方反导系统拦截，需要制定科学合理的进攻路线。通过对导弹发射过程的动态分析，并依据我国现役陆基反舰导弹（如鹰击 18）的各项参数，建立了一种适宜的轨道模型，使用 MATLAB 求解，得到了适合的轨道。

针对问题一：由于导弹发射点与航母所在点经纬度相差较小，故可以将地面其近似为平面求解。将导弹发射分为三个阶段：初始抛物线阶段、中段、末段加速阶段。中段起始于抛物线顶点，再细分为三个阶段：向下抛物线阶段、竖直方向减速阶段（最终竖直方向减速为 0）、超低空巡航段（为使导弹避开拦截，采用超低空巡航模式，高度约为 60m）。在末段从原速度加速到 1000m/s，打中目标。

针对问题二：在问题一的基础上，导弹在中段的巡航段进行精确制导，即导弹的速度方向始终指向航母。经过计算，导弹在 20s 内从巡航速度加速到最高速度所走的路程约为 6 至 7km，故巡航阶段结束时导弹与航母距离 d＜6km，导弹可以通过自主导航在 20s 内击中目标。由此建立导弹运动的轨迹模型，分析中段结束时导弹能否飞到距航母 6km 以内。

针对问题三：在问题一、二的基础上，不经过末段自主制导，此时判断导弹与航母距离随时间的变化（从 6000m 到末尾处）。考察若不经过导弹自主制导而依靠中段导航能否击中目标。修改初始轨道参数，判断导弹打击航母的命中率。分析导弹在其他条件影响下的命中率。

关键词：导弹制导 最优路线 导弹突防 命中概率

一、问题重述

请根据如下的已知条件和有关数据，设计导弹运行的数学模型及其命中目标的算法：

导弹发射车初始位置坐标已知为东经 120°30′0"，北纬 27°30′0",它可直接设为导弹打击航母的坐标系原点。

(1)由海洋侦察卫星与高空长航时无人机侦察，传输给陆基导弹发射指挥中心计算确定的航母初始位置坐标 H (X0,Y0) 为东经 123°45′0"，北纬 25° 39′0"。航母的舰长为 335m,航速保持为 32 节(1 节=1.852km/h),航向始终为正南方向。航母的动态坐标数据 H(X0,Y0)由卫星和无人机动态提供给指挥中心，动态监控数据记为 Hi(X(ti),Y(ti)),i=1，2，...n...指挥中心由此可建模计算航母的速度和航行轨道，同时计算导弹打击航母命中的动态运行轨道。

  1. 导弹运行的轨道曲线划分为发射段，中段和末段。发射段通常为抛物线，发射速度为 500m/s。中段可设计为不同的飞行轨道，由导弹的飞行参数制导所确定。末段最高速度可达到 1000m/s。导弹末段飞行时间般不超过 20 秒。段曲线的衔接点是光滑的(即曲线连续且一阶导数存在)，也就是说导弹飞行的轨道曲线是连续和光滑的，不能折线飞行。

  2. 导弹运行的轨道曲线需考虑应对敌方反导系统拦截问题，期望给出难以拦截的攻击曲线。

  3. 地面指挥中心提供给导弹中段轨道的制导数据; 而末段则是由导弹自主攻击航母目标。

  4. 其它复杂环境及气象等影响暂且简化

  5. 解题可局部自主创新添加合理假设.

  6. 在建模设计的算中，根据坐标计算距离时，设定地球半径为 6300km 距离的计算精度要求为 m 级。

根据以上已知数据和条件要求，请你运筹帷幄，决胜千里，创新设计出你的陆基反舰导弹打击航母的运行轨道数学模型，论述你的算法步骤。包括:

问题 1: 建立初始状态下，反舰导弹打击航母的静态轨道模型。即 t=0 时，连接导弹初始位置与航母坐标之间的轨道曲线模型。

问题 2: 在航母按照已知条件(1)给出的航向和速度的航行状态下，设计导弹飞行的中段动态模型方程和算法步骤。中段通常以发射段的抛物线顶点为起始点。

问题 3: 讨论你所设计的导弹打击航母的轨道自线的误差分析和命中率分

二、模型假设

1.假设导弹初段末高度为 10km

2.假设导弹在 75s 时启动推进器在竖直方向减速

3.假设导弹末段加速度为 70m/s2

4.假设导弹不受到其他因素（如风、电磁干扰等等）

三、符号说明

符号 意义
t1 导弹初段末时刻（s）
t2 导弹开始竖直方向减速的时刻（s）
t3 导弹进入超低空水平巡航的时刻（s）
x1 z1 导弹初段末坐标（m）
x2 z2 导弹开始竖直方向减速的坐标（m）
x3 z3 导弹进入超低空水平巡航的坐标（m）
k 导弹运动的总时间（s）
a(x,y,z) 导弹巡航阶段追击的坐标（m）
b(x,y,z) 航母的坐标（m）
d 导弹与航母的距离（m）

四、问题分析

针对问题一：将导弹发射分成初段、中段、末段，中段再细分为抛物段、减速段、巡航段。为避免被反导雷达发现，将其布置为超低空巡航。并于末段加速到 1000m/s 打击目标。

针对问题二：在第一问的基础上，在中段巡航段令导弹速度始终指向航母，建立导弹的运行模型，经过计算，导弹在 20s 内从巡航速度加速到最高速度所走的路程约为 6 至 7km，故巡航阶段结束时导弹与航母距离 d＜6km，分析导弹能否运行至距航母 6000m 以内。

针对问题三：在一二问的基础上分析导弹能否在不经过末段自主导航就成功命中目标，并分析如何修改参数能使命中精度最高。分析其他条件对命中率的影响。

五、模型建立及求解

5.1 问题 1 静态轨道

5.1.1 问题分析

图一 问题的分析过程

5.1.2 模型建立

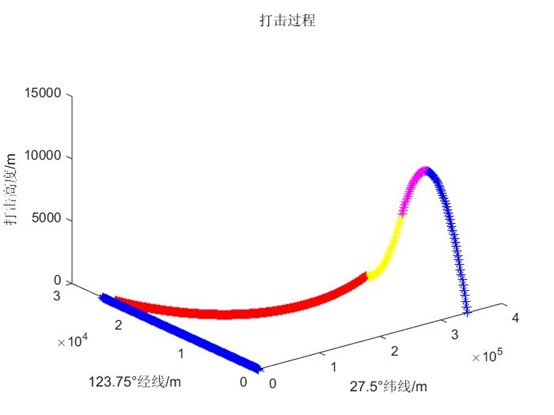
问题一为初始条件下，求解反舰导弹弹打击航母的静态轨道模型，由于导弹发射点与航母所在点经纬度相差较小，将模型建立在在二维平面内，并且是点对点的静态模型。分三段分析导弹的飞行过程，分别为发射段，中段和末段， 其中， 中段起始于抛物线顶点，再细分为三个阶段：向下抛物线阶段、竖直方向减速阶段（最终竖直方向减速为 0）、超低空巡航段（为使导弹避开拦截，采用超低空巡航模式，高度约为 60m）。在末段从原速度加速到1000m/s，打中目标。

5.1.2.1 两点间距离模型

首先确定发射点和打击点的平面距离，将地球抽象为一个球体，两点即为球面上两点的直线距离。利用公式，设所求点 A ，纬度 β1 ，经度 α1 ；点 B ，纬度 β2 ，经度 α2。则距离 S=R·arc cos[cosβ1cosβ2cos（α1-α2）+sinβ1sinβ2]，其中 R 为球体半径。

利用 matlab 求解此直线距离。

5.1.2. 2 发射段飞行模型

根据资料表明[1]，导弹需发射到 10000m 的左右高度。故将初速度分为水平方向和竖直方向。水平速度为…√5×100,竖直方向速度为√21×100m/s

（1）发射段为向上抛物线阶段。炮弹在竖直方向上做匀减速运动，竖直初速度为√20×100m/s,末速度为零。在水平方向上一直做匀速直线运动。轨迹为抛物线。

（2）向下抛物线阶段。

到最高点之后，炮弹先按原轨迹抛物线运动，仍以原加速度运动，竖直方向为自由落体运动，水平方向上，仍以原速度运动。

（3）竖直方向减速阶段

至 t=75s(时间为假设时间)时，改变运动轨迹，以向下的加速度 a=7m/s（根据资料查阅可知，导弹的减速加速度为 7m/s)水平速度不变。使至水平方向时竖直方向速度为 0。

（4）根据已知数据及轨迹分析，利用公式 x=vt-1/2at^2 及 v=at，并用 matlab 绘制出图线。

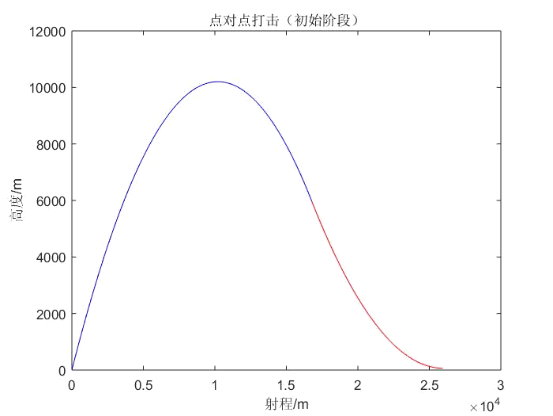
图二 发射段轨迹图线

（蓝线部分为抛物线轨迹，红线部分，改变加速度，水平速度不变，到贴近水平面的超低空飞行，以应对敌方导弹拦截。[2]）

5.1.2.3 低空巡航模型

在导弹飞行过程中，为躲避对方导弹拦截，采用超低空巡航模式，高度约为 60m）。在末段从原速度加速到 1000m/s，打中目标。

炮弹经过竖直减速阶段，竖直速度已经非常低几乎可以忽略不计。水平方向上，理论上（忽略风力，温度气象等阻力）仍是√5×100m/s 距离水平面60m/s。

进行水平的直线运动。

导弹末段飞行时间不超过 20s，且末段速度最大达到 1000m/s，所以要在水平阶段先保持 223.60m/s 的速度，水平方向上保持直线运动。经过查阅可知，导弹的加速度在加速阶段一般保持在 70m/s 左右，故水平加速度取为 70m/s，末段从 223.60m/s 加速到 1000m/s 。

利用公式 v=at 及 matlab 绘图软件求得总体轨迹图线

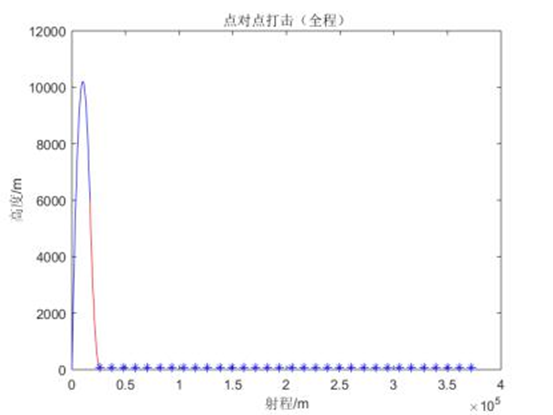
图三 全过程打击图线

5.2 问题 2 设计导弹飞行的中段动态模型方程和算法步骤

5.2.1 问题分析

图四 问题的分析过程

5.2.2 模型建立

要求在已知航向和速度的航行状态下，设计导弹飞行的中段动态模型方程该问题的核心解决思路是导弹时刻对准敌机以及导弹尽量在超低空掠海航

线上行驶会尽可能避免雷达的侦测和反导系统的拦截。

5.2.2.1 发射段飞行模型

首先第一阶段的函数与问题一相同，从第一段抛物线顶点开始进行第二阶段，首先是开口向下抛物线改变轨迹，然后是开口向上抛物线让导弹的竖直速度降低为 0.两段抛物线轨迹为：

1.x=Vxt;z=Vzt-(1/2)(9.8)t^2

2.x=Vxt;z=z2+Vz2(t-t2)+0.5a(t-t2)^2

5.2.2.2 定向追击模型

然后进行中段定向追击。中端追击过程中，需要导弹和航母的实时坐标，而导弹的方向及坐标由航母确定。考虑到xy平面是以静态航母和导弹初始位置连线为X轴，而航母运动方向为正南并不以x轴衡量，故需建立南方向与x轴y轴的方向关系。

在北纬27.5°的纬度圈上，导弹与航母的经度差为3.25°。由RCos27.5°求得纬度圆半径为5651.2km。则该经度差对应球面上的距离为

2π5651.23.25/360=320.39km。由此得出正南方向与已知坐标系的想轴夹角的正弦值为0.8466，即夹角近似为58°。角度已知，则航母的正南方向运动能正确体现在坐标轴分量上。

假设航母航行距离极短，则此时地球可视为平面，利用x=v*t，求得航母航向的距离，得到其位置坐标，从而求得航母与导弹之间的实时距离。

这是超低空巡航的两个重要参数。通过初始状态下导弹坐标，实时母舰坐标推导出导弹到母舰的方向向量从而确定导弹接下来的轨迹与方向，从而实现导弹任意时刻朝向母舰，同时，为保证模型简化，并最终在第二阶段结束时靠近母舰使与其距离不大于 6km

5.2.2.3 主要转折点坐标

重要点 k a b d
第二阶段起点 k=46 a(334392.97,5403.27,10202.11) b(0,740.80,0) d=334581.05
两抛物线交点 k=5 a(328586.85,8841.44,6362.48) b(0,1212.18,0) d=328736.98
超低空巡航起点 k=116 a(320401.84,13688.29,78.35) b(0,1876.69,0) d=320619.49
超低空巡航终点 k=1528 a(5442.74,23686.95,1.07) b(0,25123.20,0) d=5852.66

表一：主要转折点坐标

5.2.2.4 模型示意图

图五 全程模型

5.3 问题 3 误差分析

5.3.1 分析无自主制导 d<6000m 时 d 随 k 的变化

将停止条件设为导弹高度小于 0，此时判断导弹与航母距离随时间从 6000m 到末尾处的变化：

k=1528 a(5442.74,23686.95,1.07) b(0,25123.20,0) d=5852.66
k=1529 a(5226.70,23744.61,1.02) b(0,25139.66,0) d=5633.28
k=1530 a(5010.83,23802.91,0.98) b(0,25156.12,0) d=5413.94
k=1531 a(4795.13,23861.87,0.94) b(0,25172.59,0) d=5194.65
k=1532 a(4579.63,23921.51,0.90) b(0,25189.05,0) d=4975.41
k=1533 a(4364.32,23981.88,0.86) b(0,25205.51,0) d=4756.22
k=1534 a(4149.23,24043.00,0.81) b(0,25221.97,0) d=4537.09
k=1535 a(3934.36,24104.90,0.77) b(0,25238.44,0) d=4318.01
k=1536 a(3719.74,24167.64,0.73) b(0,25254.90,0) d=4098.99
k=1537 a(3505.37,24231.24,0.69) b(0,25271.36,0) d=3880.03
k=1538 a(3291.28,24295.78,0.65) b(0,25287.82,0) d=3661.14
k=1539 a(3077.48,24361.29,0.60) b(0,25304.28,0) d=3442.32
k=1540 a(2864.01,24427.84,0.56) b(0,25320.75,0) d=3223.58
k=1541 a(2650.89,24495.51,0.52) b(0,25337.21,0) d=3004.91
k=1542 a(2438.15,24564.38,0.48) b(0,25353.67,0) d=2786.33
k=1543 a(2225.84,24634.54,0.44) b(0,25370.13,0) d=2567.84
k=1544 a(2014.00,24706.12,0.39) b(0,25386.60,0) d=2349.45
k=1545 a(1802.68,24779.24,0.35) b(0,25403.06,0) d=2131.17
k=1546 a(1591.97,24854.08,0.31) b(0,25419.52,0) d=1913.01
k=1547 a(1381.96,24930.85,0.27) b(0,25435.98,0) d=1694.99
k=1548 a(1172.75,25009.81,0.23) b(0,25452.44,0) d=1477.11
k=1549 a(964.53,25091.32,0.19) b(0,25468.91,0) d=1259.41
k=1550 a(757.53,25175.89,0.15) b(0,25485.37,0) d=1041.92
k=1551 a(552.13,25264.27,0.11) b(0,25501.83,0) d=824.68
k=1552 a(349.00,25357.73,0.07) b(0,25518.29,0) d=607.77
k=1553 a(149.58,25458.88,0.03) b(0,25534.76,0) d=391.33
k=1554 a(-40.69,25576.34,-0.01) b(0,25551.22,0) d=175.78

表二：导弹与航母距离随时间从 6000m 到末尾处的变化

由表格得知，当导弹距水面为 0.03m 时，距航母仍有 391.33m，大于航母的舰长 335m，故若无末段自主制导，将无法击中航母。

5.3.2 分析命中精度与 t2 的关系

改变飞行参数再次运行，此时将初段抛物线轨道参数改变，将中段竖直向下减速段起始时间 75s 进行修改，在不同情况下的运行结果如下表：

t2=60s k=1552s a(151.59,25440.48,1.54) b(0,25518.29,0) d=394.00m
t2=61s k=1553 a(-26.93,25551.16,-0.26) b(0,25534.76,0) d=192.08m
t2=62s k=1553 a(-15.41,25543.97,-0.14) b(0,25534.76,0) d=205.66m
t2=63s k=1553 a(-3.74,25536.95,-0.03) b(0,25534.76,0) d=219.27m
t2=64s k=1553 a(8.07,25530.09,0.07) b(0,25534.76,0) d=232.93m
t2=65s k=1553s a(20.03,25523.34,0.15) b(0,25534.76,0) d=246.66m
t2=70s k=1553s a(82.19,25490.81,0.35) b(0,25534.76,0) d=316.81m
t2=71s k=1553s a(95.18,25484.43,0.34) b(0,25534.76,0) d=331.28m
t2=72s k=1553s a(108.40,25478.06,0.30) b(0,25534.76,0) d=345.94m
t2=73s k=1553s a(121.86,25471.68,0.24) b(0,25534.76,0) d=360.82m
t2=74s k=1553s a(135.58,25465.30,0.15) b(0,25534.76,0) d=375.94m

表三：打击精度随 t2 的变化

由表可知，当 t2=61s 时打击精度最高，二者距离仅为 192.08m

导弹末端命中概率分析[3]：反舰导弹末段自主制导的命中概率，取决于制导雷达捕捉到目标的可能性，它与导弹雷达搜索区能覆盖到目标的概率与雷达能收到回波的概率有关。即 P 捕捉=P 覆盖·P 发现.且现代雷达比较灵敏，只要覆盖就能搜索到目标，故有 P 捕捉=P 覆盖，即 P 发现.=1。

为方便分析,将导弹搜索区域简化成矩形区域，且设导弹的自控终点是一个

沿 X 轴和 Z 轴方向分布的二维随机变量,服从平面上的正态分布律且互不相关时,计算 P 捕捉的公式可以简化为

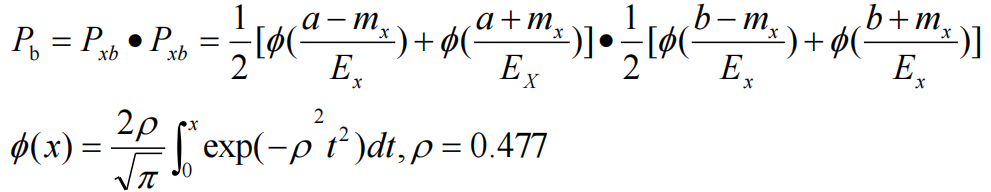
式中：a 为导弹搜索区的距离半长，单位(m);b 为导弹搜索区的侧向半宽,单位(m);Ex 为纵向综合散布概率偏差,单位(m);Ez 为侧向综合散布概率偏差,单位(m);mx 为目标运动和常值风干扰引起的纵向概率偏差,单位(m);mz 为目标运动和常值风干扰引起的侧向概率偏差,单位(m)。

由此可以计算出命中概率。

六、模型评价与改进

该型未将风速及不同高度处的空气阻力考虑在内，同时在路程及范围较小情况下未考虑地心引力。会对模模型的精确度造成一定误差。除此之外，假设不变的参量还有母舰运行时距离极小，将距离与纬度近似成为正比关系；角度运算中将小数位四舍五入或忽略误差等。在算法方面，卫星及无人机的传输数据有一定的时间延后性，且进行导弹永远朝向母舰的拟合过程中，取 1 秒为间隔时间也对最终第三阶段的自主攻击增大了误差的可能性。

但总的来说，该模型最大的优点是没有使用复杂曲线的方式来闪避反导拦截而是采用科技上惯用的躲避方式，使雷达不易勘测。除此之外，轨迹变换，速度

变化，点对点定向等处理方式也体现了数学模型省略不必要因素，简单明了的表达被表达物体运行特性的特点。同时，该模型对一些未知参量的选取也尽可能满足现实和近期的科技发展。例如，在第一阶段抛物线的顶点高度设置为 10km，该高度为对流层高度，并且是一般陆基导弹的第一阶段能达到的高度。并且第二阶段整体的时间设定 6 到 8 分钟也符合现实陆基导弹攻击的第二阶段时间。这样的处理方式让依照时间推算出的速度变化有了更高的可信度。同时使超低空巡航阶段的速度不变有了一定得依据。最后，现在一般的路基导弹的第三阶段自主攻击时间一般为 20 秒左右或更少，这也是第二阶段拟合速度，高度，距离的依据。

但该模型的缺点是远距离能避开雷达的侦测使导弹能相对安全的接近母舰附近，但近距离的反导拦截仍不能避免，该导弹在刚进入三阶段开始自主攻击时，有被拦截的危险。所以在二阶段的末端应增加一个小阶段，该阶段拥有较为复杂的轨迹而不是简单的点对点定向接近母舰。初步思路为在点对点定向之后导弹再次做类似于开口向上的抛物线运动在 z 轴方向远离母舰同时在 xy 轴方向靠近，闪避反导系统拦截，再做轨迹为开口向下的抛物线运动然后攻击母舰，期间导弹加速。这样的设计给雷达的侦测带来了困难同时也使一旦被雷达成功侦测后的闪避提供了更大可能，增加了成功率。同时，这一阶段的缓冲，也能让导弹更精确的攻击到舰体。

七、参考文献

[1] Honeywell，《世界七大反舰导弹：祖国排名第一》， https://m.baidu.com/paw/c/m.tiexue.net/touch/thread_8238501_1.html%3F mip ，2018.05.01。

[2] 飞行员梦，《已发射的导弹如何反拦截》， https://zhidao.baidu.com/question/519956706.html ，2018.04.30。

[3] 聂永芳、冯林平、施建礼，新误差分析方法对反舰导弹作战使用的影响，《舰船电子工程》，卷期号：2012 年第七期，总第 217 期，57-59，2012

附录

问题一程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
A=25.65*pi/180;B=123.75*pi/180;C=27.5*pi/180;D=120.5*

pi/180;

S=6300000*acos(cos(A)*cos(C)*cos(B-D)+sin(A)*sin(C));

Vx=sqrt(5)*100;Vy=sqrt(20)*100;

t1=Vy/9.8; x1=Vx*t1; y1=Vy*t1-0.5*9.8*t1^2; x2=Vx*75;

y2=Vy*75-0.5*9.8*75^2;

t2=75;

t=0:t2;

x=Vx*t;y=Vy*t-0.5*9.8*t.^2;

plot(x,y,'b');

hold on

a=7;

Vy2=Vy-9.8*75;t3=t2-Vy2/a;

t=t2:t3;

x=Vx*t;y=y2+Vy2*(t-t2)+0.5*a*(t-t2).^2;

plot(x,y,'r');

hold on

Vy3=Vy2+a*(t3-t2);x3=Vx*t3; y3=y2+Vy2*(t3-t2)+0.5*a*(t3-t2)^2;

fprintf('x1=%.4f y1=%.4f t1=%.4f\nx2=%.4f y2=%.4f t2=%.4f Vy2=%.4f\nx3=%.4f y3=%.4f t3=%.4f Vy3=%.4f \n ',x1,y1,t1,x2,y2,t2,Vy2,x3,y3,t3,Vy3) Vx=223.6068;

t_5=(1000-Vx)/70; x_5=Vx*t_5+0.5*70*t_5^2;

t4=(S)/Vx;x4=Vx*t4

t=t3:50:t4;

x=Vx*t;y=y3;

plot(x,y,'b*')

hold on

t5=t4+t_5;

t=t4:t5;

x=x4+Vx*(t5-t4)+0.5*70*(t5-t4)^2;

plot(x,y,'r')

xlabel('Éä³Ì/m');

ylabel('¸ß¶È/m');

title('µã¶Ôµã´ò»÷');

问题二程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
A=25.65*pi/180;B=123.75*pi/180;C=27.5*pi/180;D=120.5*

pi/180;

S=6300000*acos(cos(A)*cos(C)*cos(B-D)+sin(A)*sin(C));

Vx=sqrt(5)*100;Vz=sqrt(20)*100;

t1=Vz/9.8; x1=Vx*t1; z1=Vz*t1-0.5*9.8*t1^2;

t2=75;x2=Vx*t2; z2=Vz*t2-0.5*9.8*t2^2;

aa=7;Vz2=Vz-9.8*75;

t3=t2-Vz2/aa;x3=Vx*t3;z3=z2+Vz2*(t3-t2)+0.5*aa*(t3-t2)^2;

Vz3=Vz2+aa*(t3-t2);

r=6300000*sin(27.5-25.65);

X=(123.75-120.5)/360*2*r*pi;Y=(27.5-25.65)/360*2*6300000*pi;

m=Y/S;n=X/S;

k=0;v=32*1852/3600;

for t=0:1:t1

x=X-n*Vx*t;y=m*Vx*t;z=Vz*t-0.5*9.8*t^2;

plot3(x,y,z,'b*');

hold on

s=v*t;

plot3(0,s,0,'b*');

%pause(0.2);

k=k+1;

d=sqrt(x^2+(y-s)^2+z^2);

fprintf('k=%.0f a(%.2f,%.2f,%.2f) b(0,%.2f,0) d=%.2f\n',k,x,y,z,s,d);

xlabel('27.5¡ãγÏß/m');

ylabel('123.75¡ã¾-Ïß/m');

zlabel('´ò»÷¸ß¶È/m');

title('´ò»÷¹ý³Ì');

end

for t=t1:1:t2

x=X-n*Vx*t;y=m*Vx*t;z=Vz*t-0.5*9.8*t^2;

plot3(x,y,z,'m*');

hold on

s=v*t;

plot3(0,s,0,'b*');

%pause(0.2);

k=k+1;

d=sqrt(x^2+(y-s)^2+z^2);

fprintf('k=%.0f a(%.2f,%.2f,%.2f) b(0,%.2f,0) d=%.2f\n',k,x,y,z,s,d);

end

for t=t2:1:t3

x=X-n*Vx*t;y=m*Vx*t;z=z2+Vz2*(t-t2)+0.5*aa*(t-t2)^2;

plot3(x,y,z,'y*');

hold on

s=v*t;

plot3(0,s,0,'b*');

%pause(0.2);

k=k+1;

d=sqrt(x2+(y-s)^2+z^2);

fprintf('k=%.0f a(%.2f,%.2f,%.2f) b(0,%.2f,0) d=%.2f\n',k,x,y,z,s,d);

end

a=[(X-n*x3),(m*x3),z3];b=[0,v*t3,0];

dt=1;d=sqrt(a(1)^2+(a(2)-b(2))^2+a(3)^2);

while d>6000

plot3(a(1),a(2),a(3),'r*');

hold on

plot3(b(1),b(2),b(3),'b*');

%pause(0.2);

k=k+1;

b=b+[0,v*dt,0];

e=b-a;

d=norm(e); e0=e/d;

a=a+Vx*dt*e0;

fprintf('k=%.0f a(%.2f,%.2f,%.2f) b(0,%.2f,0) d=%.2f\n',k,a(1),a(2),a(3),b(2),d);

end
本站总访问量次 | 您是第位访客