2018-06-02

数学实验报告

全文共: 7k字 | 阅读时长: 32分

阅读

文章导航

大一下数学实验报告（书后题目）

做得较好的题目：第四次任务第一题 P15

第一次任务

实验八练习一 2.

① 实验问题：

某车间有甲·乙·丙三台车床可用于加工零件，这三台车床可用于工作的最多时间分别为700h，800h 和 900h，需要加工的三种零件的数量分别为 300，400 和 500。不同车床加工不同零件所用时间和费用如下表所示，在完成任务的前提下，如何分配加工任务，才能使加工费最少？

车床名称	加工	单位零件	所需时数	加工	单位零件	所需费用	可用于工作的时数
	零件1	零件2	零件3	零件1	零件2	零件3
甲	0.4	0.5	0.5	7	8	8	700
乙	0.8	0.7	0.5	8	7	8	800
丙	0.8	0.6	0.6	7	9	8	900

②问题分析：该题是一道一般线性规划问题，决策变量个数为 9，限制条件为 3 个不等式和 3 个等式，整理后运用 linprog 函数即可求解。

③程序设计流程图：

f=[7,8,7,8,7,9,8,8,8];

a=[0.6,0,0,0.5,0,0,0.5,0,0;0,0.4,0,0,0.7,0,0,0.5,0;0,0,0.8,0,0,0.6,0,0,0.6];

b=[700,800,900];

aeq=[1,1,1,0,0,0,0,0,0;0,0,0,1,1,1,0,0,0;0,0,0,0,0,0,1,1,1];

beq=[300,400,500];

vlb=[0,0,0,0,0,0,0,0,0];

vub=[];

[x,fval]=linprog(f,a,b,aeq,beq,vlb,vub)

答案

x =

103.7917

0.0000

196.2083

0.0000

400.0000

0.0000

149.9740

151.1015

198.9245

fval =

8.9000e+003

④结果分析与结论：所以应当用甲车床生产 104 件零件 1，196 件零件 3；用乙车床生产 400 件零件 2；用丙车床生产 150 件零件 1,151 件零件 2,199 件零件 3. ⑤总结与体会：该题的核心是确定各个变量在矩阵中的位置。第一次做时，因变量位置看错，导致了结果错误，检查改正后结果正常。

实验八练习一 5.

① 实验问题:

某医院每日至少需要护士人数如下表所示。

班次	时间段	人数
1	6:00~10：00	60
2	10:00~14:00	70
3	14:00~18:00	60
4	:18:00~22:00	50
5	22:00~2:00	20
6	2：00~6:00	30

每班护士在值班开始时向病房报到，连续工作 8h，医院至少需要多少少护士才能满足值班要求？

②问题分析：本题为一般线性规划问题，决策变量个数为 6，限制条件位 6 个不等式，之后运用 linprog 函数可求解。

③程序设计流程图：

c=[1,1,1,1,1,1];

a(1,:)=[-1,0,0,0,0,-1];

a(2,:)=[-1,-1,0,0,0,0];

a(3,:)=[0,-1,-1,0,0,0];

a(4,:)=[0,0,-1,-1,0,0];

a(5,:)=[0,0,0,-1,-1,0];

a(6,:)=[0,0,0,0,-1,-1];

b=[-60;-70;-60;-50;-20;-30];

[c,fval]=linprog(c,a,b)

结果

c =

35.2410

34.7590

28.7310

21.2690

1.1272

28.8728

fval =

150.0000

④结果分析与结论：所以至少需要 150 个护士才能满足要求。⑤总结与体会：该题是一道简单的一般线性规划问题，确定决策变量个数后即可快速求解。

实验八练习二 2.

①实验问题：某校学生在大学三年级第一学期必须要选修的课程（必修课）只有一门（2 个学分）;可供限定选修的课程有 8 门，任意选修课程有 10 门。由于一些课程之间忽悠联系，所以可能在选修某门课程中必须同时选修其他课程，这 18 门课程的学分数和要求同时选修课程的相应信息如下表所示。

课程信息表

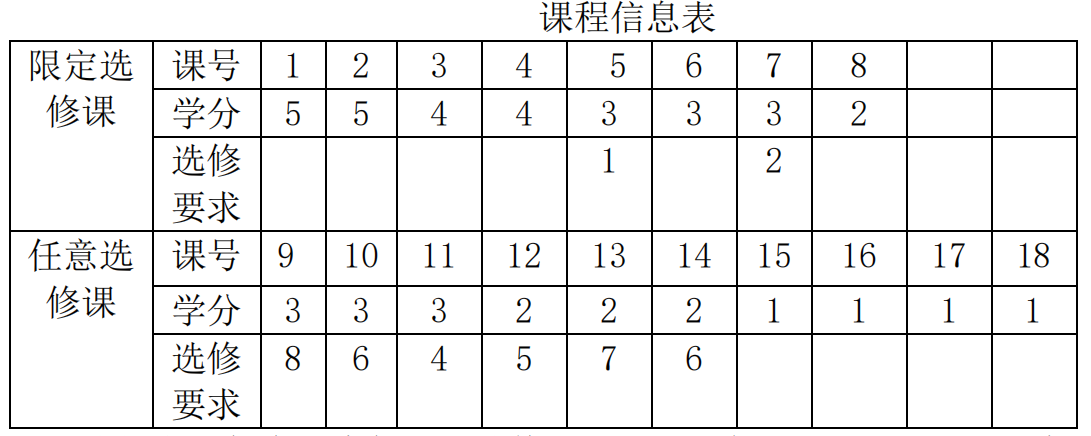
按学校规定，每个学生每学期选修的总学分不能少于 21 学分，因此，学生必须在上述 18 门课程中至少选修 19 学分，学校同时还规定学生每学期选修任意选修课的学分不能少于 3 学分，也不能超过 6 学分。为了达到要求，试为该学生确定一种选课方案。

②问题分析：本题是一道 0-1 规划问题，难点主要在于，选了 y 一定要选 x，

但选了 x 可以选 y 也可以不选 y，故本题需要更改计算方式，考虑 X-Y≥0 即可

解决问题。

③程序设计流程图：

c=[-5,-5,-4,-4,-3,-3,-3,-2,-3,-3,-3,-2,-2,-2,-1,-1,-1,-1]; a=[-5,-5,-4,-4,-3,-3,-3,-2,-3,-3,-3,-2,-2,-2,-1,-1,-1,-1;
0,0,0,0,0,0,0,0,3,3,3,2,2,2,1,1,1,1; 0,0,0,0,0,0,0,0,-3,-3,-3,-2,-2,-2,-1,-1,-1,-1; -1,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0; 0,-1,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0; 0,0,0,0,0,0,0,-1,1,0,0,0,0,0,0,0,0,0; 0,0,0,0,0,-1,0,0,0,1,0,0,0,0,0,0,0,0; 0,0,0,-1,0,0,0,0,0,0,1,0,0,0,0,0,0,0; 0,0,0,0,-1,0,0,0,0,0,0,1,0,0,0,0,0,0; 0,0,0,0,0,0,-1,0,0,0,0,0,1,0,0,0,0,0;
0,0,0,0,0,-1,0,0,0,0,0,0,0,1,0,0,0,0]; b=[-19;6;-3;0;0;0;0;0;0;0;0];
[x,fval]=bintprog(c,a,b);
fval=-fval
xmax=x

答案

fval =

xmax =

④结果分析与结论：由实验结果可以得出，需要连选前面的 10 门课才可以达到要求。此时的总学分已远远超出学校要求，但仍为最佳方案。

⑤总结与体会：在做本题时，开始是使用了一般线性规划的方法，但未成功，经过翻书查找，最后确定了该规划的类型以及求解方法。

实验九 3.

①实验问题：某企业在两个相互分离的市场上出售同一产品，两个市场的需求哈密数分别为 p1=18-2*q1,p2=12-q2,其中 p1、p2 分别表示该产品在两个市场上的价格(单位:万元/t)，q1、q2 分别表示该产品在两个市场上的销售总量，即 q=q1+q2。在产销平衡的状态下:

(1)如果该企业实行价格差别战略（即 q1≠q2），试确定两个市场上该产品的

销售量和最优价格，使该企业获得最大利润。

(2)如果该企业实行价格差别战略（即 q1=q2），试确定两个市场上该产品的销售量和最优价格，使该企业获得最大利润。

②问题分析：本题的主要思路是如何编辑一个二元函数，并利用该函数求解最大值。显然，应该以销量为自变量。

③程序设计流程图：

第一问

f='-1*((18-x(1))*x(1)*0.5+(12-x(2))*x(2)-2*((18-x(1))*0.5+(12-x(2)))-5)';

x0=[0,0];

[x,fmin]=fminsearch(f,x0)

fmax=-fmin

x	=

10.0001	7.0000

答案

fmin =

-52.0000

fmax =

52.0000

第二问

f='-1*((18-x)*x*0.5+(12-x)*x-2*((18-x)*0.5+(12-x))-5)';

[x,fval]=fminbnd(f,0,100)

fmax=-fval

答案

x =

8.0000

fval =

-49.0000

fmax =

49.0000

④结果分析与结论：

（1）企业应分别定价为 10 与 7，此时的最大利润为 52 万元

（2）企业应定价为 8，此时最大利润为 49 万元

⑤总结与体会：通过本题，我从对高等数学中如何求多元函数极值有了更深的认识，同时也学会了非线性规划问题的求解技巧。

第二次任务

实验任务 1.

① 实验问题：

② 问题分析：本题仍是一个线性规划问题，不同之处在于决策变量众多，因此，经过研究决定使用表格处理数据。在变量编辑器中直接对矩阵进行编辑。最后结果的列向量中令第 1—9 号为 Xz，10—15 号为 Px，16—24 号为Cy，25—33 号为 Br，34—42 号为 Jj，43—51 号为 Jg，每个矩阵为从上到下按列的顺序编号。

③ 程序设计流程图：

A：

B：

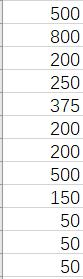
beq：

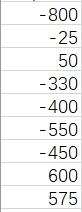
aeq：

[x1,fval1]=linprog(C1,A,B,aeq,beq,vlb,vub)

答案

x1 =

0.0000

748.0754

71.2812

0.0000

428.7188

200.0000

0.0000

500000

21.6938

0.0000

28.3062

0.0000

75.0000

39.1153

25.0000

600.0000

0.0000

175.0000

38.5548

0.0000

34.8411

34.1506

42.4535

0.0000

25.0000

0.0000

31.3100

561.4452

215.1589

203.3494

662.5465

0.0000

fval1=1.6425e+03

④结果分析与结论：结果为 1.6425e+03。

⑤总结与体会：通过该题，我学会了如何使用表格表示决策变量众多时问题的约束条件。

实验任务 2.

① 实验问题：

② 问题分析：本题仍是一个线性规划问题，不同之处在于决策变量众多，因此，经过研究决定使用表格处理数据。对于变量的编号同 1

③程序设计流程图：

[x2,fval2]=linprog(C2,A,B,aeq,beq,vlb,vub)

答案

x2 =

0.0000

800.0000

55.5556

0.0000

444.4444

200.0000

181.2588

135.0000

0.0000

175.0000

0.0000

550.0000

0.0000

600.0000

315.0000

225.0000

773.7412

0.0000

12.5176

0.0000

0.000

0.0000

fval2 =

9.6800e+05

④结果分析与结论：结果为 9.6800e+05。

⑤总结与体会：通过该题，我学会了如何使用表格表示决策变量众多时问题的约束条件。

第三次任务

实验任务 1.

1 实验问题

2 问题分析：通过循环语句对公式 a 进行计算，得到的结果与原题进行比较 3 程序设计流程图

n=50;s=0;

for k=1:n

s=s+1/(2*k-1)^2;

end

m=sqrt(8*s);

vpa(m,20)

答案：

ans =

3.1352202050631281516

4 总结分析和结论：公式 a 与原公式相比较，叠加次数均为 50 时，a 公式精度更高，所以用 a 计算 π 更好。

5 总结和体会：通过这道题目的练习，我学会了利用循环实现对无理数值的近似计算。

实验任务 2.

1 实验问题：基于关系式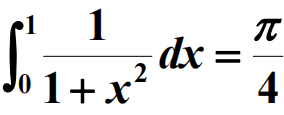利用蒙特卡洛方法近似计算 π

2 问题分析：利用 rand（1，2）产生一个二维随机数组，判断它是否在被积函数的积分范围内，用符合条件的点数除以总数乘 4 即为 π 的近似值。

3 程序设计流程图

cs=0;

n=500;

for i=1:n

a=rand(1,2);

if 1/(1+a(1)^2)>=a(2)

cs=cs+1;

end

end

m=4*cs/n

4 总结分析和结论：

N 分别为 500 5000 50000 500000 时，算得 π 的近似值分别为

3.15200000

3.15920000

3.14368000

3.14192000

5 总结和体会：

通过计算本题，我学会了如何用概率计算估计确定的值

实验任务 3

1 实验问题

用 MATLAB 完成下列实验任务

（1）求 y=cos x 在 x=0 处的泰勒展开式

（2）计算 cos1 近似值，为使精确度达到 10^(-4),要用多少次多项式代替函数 y=cos x

2 问题分析

利用求泰勒展开式的函数，即可求解。
定义变量 x,n，构造 f1,f2,为其泰勒展开式，f2,f1,差值为其误差，即 cos x 在 x=1 处的泰勒展开式的差值小于 10^（-4），求出此时的 n

3 解题程序

（1）

1
2
3

syms	x;

taylor(cos(x),x,0,'order',10)

ans =

x^8/40320 - x^6/720 + x^4/24 - x^2/2 + 1

（2）

syms	x	n,

for	n=5:100

f1=taylor(cos(x),x,'order',n)

f2=taylor(cos(x),x,'order',n+1)

if(subs(f2-f1,x,1)<=10^(-4))

fprintf('the	answer	is	%d\n',n+1)

break

end

end

f1 =

x^4/24 - x^2/2 + 1

f2 =

x^4/24 - x^2/2 + 1

the answer is 6

4 结果分析

实验结果表明，计算 cos 1 的近似值时为使精确度达到 10^(-4),至少要用 6 次泰勒多项式代替函数 y=cos x

5 总结体会

通过以上分析与实践，学会了利用 matlab 用泰勒公式对近似值求解，并且，对不同的展开项数的精确程度有一定认识。

实验任务4 练习2 1

1 题目

完成下面任务

求出函数 f(x)=e^(-x2))在 x=0 的泰勒展开式，由此计算 e 的近似值
在精确位数相同的情况下，同函数 f(x)=e^x 在 x=0 的泰勒展开式比较，吗一个计算无理数 e 所需要的选取的项数较多？

2 问题分析

1）用 matlab 的函数求出泰勒展开式，并由其通项的变化规律求出其指定项数的确定精确度的 e 的近似值。

2）根据 e^x 的泰勒展开式，求出其通项，在选取项数相同的情况下，分析其精确度的差距。若其更精确，则说明 e^x 在同样的展开项数下，更接近 e 的值，即当精确位数相同时，需要的项数较少。

3 解题程序

1
2
3

syms x;

taylor(exp(-x^2),x,0,'order',10)

ans =

x^8/24 - x^6/6 + x^4/2 - x^2 + 1

he=1

ji=1

n=5

digits(25)

for k=1:n

ji=ji*k*(-1) 

he=(he+1/ji)

end

y=vpa(he,20)
e=y^(-1)

答案：

y =

0.36666666666666666667

e =

2.727272727272727272727273

（2）

he=1

ji=1

n=30

digits(25)

for k=1:n

 ji=ji*k

 he=he+1/ji

end

e=vpa(he,20)

答案：

he =

2.7183

e =

2.7182818284590455349

4 结果分析

当选取相同的项数时，e^(-x2))的精确度没有 e^x 高，所以在相同的精确度下，e^(-x2))的选取的项数较多。

5 总结体会

学会了一般型函数的泰勒展开的基本方法

用泰勒公式计算无限不循环小数的基本过程

学会了利用构造循环数列来求已知泰勒展开的项数时，求固定精确度的近似值的方法。

第四次任务

实验任务 1

1 题目

2 问题分析

（1）分别以 OB、OA 为 x 轴、y 轴的正方向建立直角坐标系，设在时刻 t，兔子的位置到达点 R（0，at），狗到达点 D（x，y）

（2）在这一过程中，兔子与狗跑的时间相同，均为120/8 = 15𝑠，故有狗跑过的路程为15 × 17.0803 = 256.2045m

（3）用计算机仿真法绘制狗与兔子的奔跑曲线，令狗的速度方向时时指向兔子，时间间隔取 0.01s，相距 0.1m 时停止。

（4）用计算机仿真法，将第一阶段停止条件设为二者相距30m，此时令其余条件与前三问相同，当距离小于 0.1m 时停止。通过调整适当的狗的初始速度，使得兔子跑的距离为 120m，此时狗的速度就为最小速度，并求出狗的匀速时间和加速时间，从而得到狗的路程。由程序得 b=15.41m/s，t1=13.8800s t2=2.2200s 所以狗的路程

3．解题程序

（1）（2）

f=inline('120(1-(8/x)^2)-200(8/x)'); b=fzero(f,[1,20])

或：

b=solve('120(1-(8/x)^2)-200(8/x)','x')

答案：

b =

17.0803

（3）

c=200; a=8; b=17.0308;n=sqrt(2)/2;

dogxb=[];dogyb=[];rabbitxb=[];rabbityb=[];

d=0.1;dt=0.1;t=0;

dogx=c;dogy=0;rabbitx=0;rabbity=0;

while (sqrt((dogx-rabbitx)^2+(dogy-rabbity)^2)>d)

t=t+dt;

dogx=dogx-b*dt*dogx/sqrt(dogx^2+(a*t-dogy)^2);

dogxb=[dogxb,dogx];

dogy=dogy+b*dt*(a*t-dogy)/sqrt(dogx^2+(a*t-dogy)^2);

dogyb=[dogyb,dogy];

rabbity=a*t;

rabbityb=[rabbityb,rabbity];

end

rabbitxb=zeros(length(rabbityb));

dogxb=-dogxb;

plot(dogxb,dogyb,'r*',rabbitxb,rabbityb,'b*')

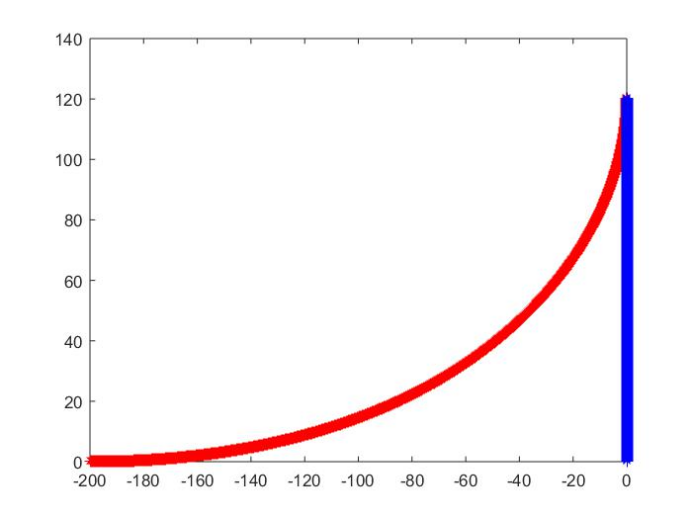
将最后一句替换为

dogx0=n.*dogxb-n.*dogyb;dogy0=n.*dogxb+n.*dogyb; 

rabbitx0=-n.*rabbityb;rabbity0=n.*rabbityb; 

plot(dogx0,dogy0, 'r*', rabbitx0,rabbity0, 'b*')

进行坐标变换即可得到题目要求的追击路线：

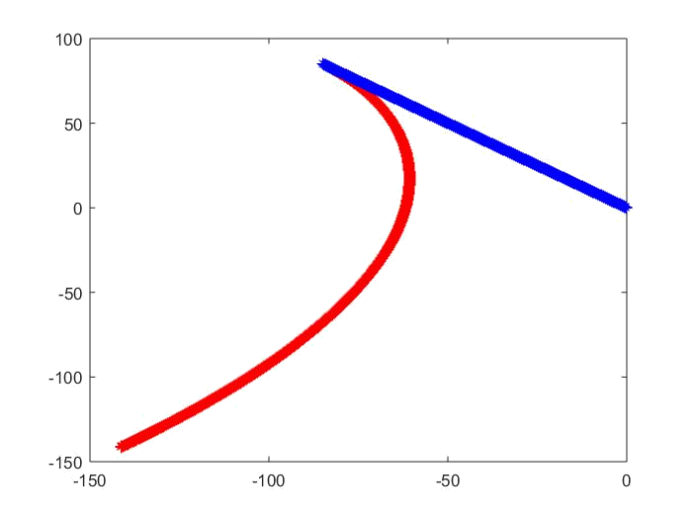
（4）

c=-200; a=8; b=15.41;n=sqrt(2)/2; dogxb=[];dogyb=[];rabbitxb=[];rabbityb=[]; d1=30;d2=0.1;dt=0.01;t=0; dogx=c;dogy=0;rabbitx=0;rabbity=0;

while (sqrt((dogx-rabbitx)^2+(dogy-rabbity)^2)>d1)

t=t+dt;

dogx=dogx-b*dt*dogx/sqrt(dogx^2+(a*t-dogy)^2);

dogxb=[dogxb,dogx];

dogy=dogy+b*dt*(a*t-dogy)/sqrt(dogx^2+(a*t-dogy)^2);

dogyb=[dogyb,dogy];

rabbity=a*t;

rabbityb=[rabbityb,rabbity];

end

rabbitxb=zeros(length(rabbityb));

dogx0=n.*dogxb-n.*dogyb;dogy0=n.*dogxb+n.*dogyb; rabbitx0=-n.*rabbityb;rabbity0=n.*rabbityb; plot(dogx0,dogy0, 'r*', rabbitx0,rabbity0, 'b*') t

hold on

t=0;dogxb=[];dogyb=[];rabbitxb=[];rabbityb=[];

while (sqrt((dogx-rabbitx)^2+(dogy-rabbity)^2)>d2)

a=a*(0.5)^dt;b=b*1.1^dt;

t=t+dt;

rabbity=rabbity+a*dt;

rabbityb=[rabbityb,rabbity];

dogx=dogx-b*dt*dogx/sqrt(dogx^2+(rabbity-dogy)^2);

dogxb=[dogxb,dogx];

dogy=dogy+b*dt*(rabbity-dogy)/sqrt(dogx^2+(rabbity-dogy)^2);

dogyb=[dogyb,dogy];

end

rabbitxb=zeros(length(rabbityb));

dogx0=n.*dogxb-n.*dogyb;dogy0=n.*dogxb+n.*dogyb;

rabbitx0=-n.*rabbityb;rabbity0=n.*rabbityb;

plot(dogx0,dogy0, 'b', rabbitx0,rabbity0, 'r')

rabbity

t

运行结果：

t =

13.8800

（匀速运动时间）

rabbity =

120.0729

（兔子跑的距离）

t =

2.2200

（加速时间）

求 s：

syms t;

s1=13.88*15.41;

s2=int('15.41*1.1^t',t,0,2.22);

s=s1+s2

答案：s =251.9896026444088249314017140895

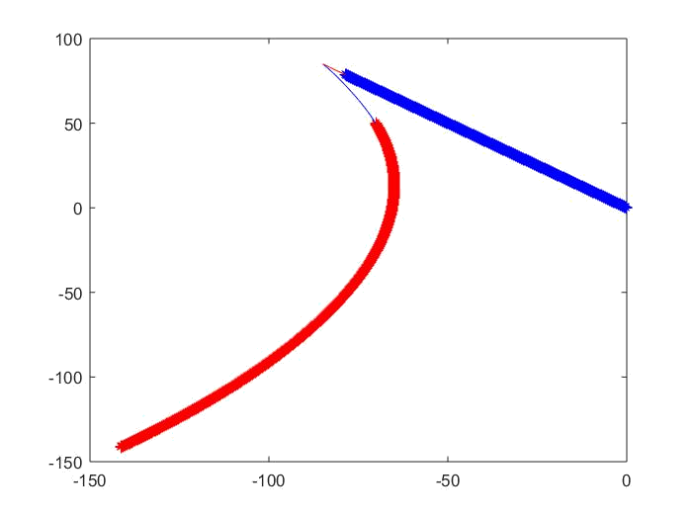
4 结果分析

（1）狗的最小速度为 17.0803m/s （2）狗的路程为 256.2045m （3）如上图（4）狗的最小速度为 15.41m/s 路程为 251.9896m 路线图如上

5 总结体会

通过这样的一次大型实验，我对于微分方程有了更加深刻的认识，同时也尝试使用 matlab 求微分方程的解析解与数值解，不过就本实验来说用仿真更加便捷。在这个过程中我对于计算机仿真、微分方程求解的能力都有了很大提高。

实验任务 2

1 实验问题

使用计算机仿真方法求解下述问题：在正方形的四个顶点上各有一人，如下图所示，在某一时刻，四人同时出发以匀速按顺时针方向追赶下一个人,如果他们始终保持对准目标,试确定每个人的行进路线。

2问题分析

本题是一个动态追击问题,我们可以通过使追及过程离散化的方法来模拟四人的追及过程,即以极短的时间段 dt 为间隔,逐步分析四人的运动状况。

3 程序设计流程图

A=[0,0];B=[0,1];C=[1,1];D=[1,0];

k=0;

dt=0.004;v=1;

grid;

hold on;

axis([0 1 0 1]);

while k<10000

k=k+1;

plot(A(1),A(2),'g.');

plot(B(1),B(2),'r.');

plot(C(1),C(2),'y.');

plot(D(1),D(2),'b.');

e1=(B-A)/norm(B-A);

A=A+v*dt*e1;

e2=(C-B)/norm(C-B);

B=B+v*dt*e2;

e3=(D-C)/norm(D-C);

C=C+v*dt*e3;

e4=A-v*dt*e1-D;d4=norm(e4);

e4=e4/d4;

D=D+v*dt*e4;

d1=norm(B-A);

d2=norm(B-A);

d3=norm(D-C);

d4=norm(A-D);

fprintf('k=%.0f d1=%.4f d3=%.4f d4=%.4f\n',k,d1,d2,d3,d4);

fprintf('A(%.2f,%.2f) B(%.2f,%.2f) C(%.2f,%.2f) D(%.2f,%.2f)\n',A(1),A(2),B(1),B(2),C(1),C(2),D(1),D(2)); if d1<=0.005

break

end

if d2<=0.005

break

end

if d3<=0.005

break

end

if d4<=0.005

break

end

pause(0.01)

end

4 结果分析和结论：

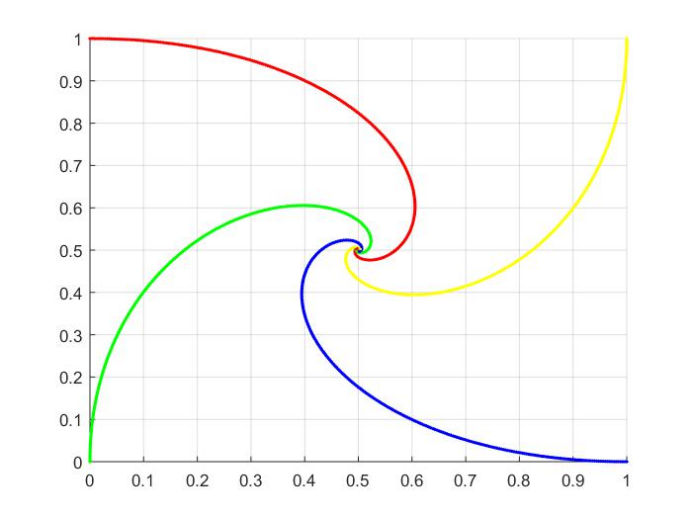
5 总结和体会：

通过这次实验，我对于计算机仿真有了更深入的理解，也掌握了更加行之有效的方法。

第五次任务

实验任务 1

题目：下表中，X 是华氏温度，Y 是一分钟内一只蟋蟀的鸣叫次数，试用多项式模型拟合这些数据，画出拟合曲线，分析你的拟合模型是否很好？

观测	序号	1	2	3	4	5	6	7	8	9	10
X	46	49	51	52	54	56	57	58	59	60
Y	40	50	55	63	72	70	77	73	90	93
观测	序号	11	12	13	14	15	16	17	18	19	20
X	61	62	63	64	66	67	68	71	72	71
Y	96	88	99	110	113	120	127	137	132	137

分析过程

上述问题为最佳曲线拟合问题，即确定一条曲线使它和实验数据点最接近，用 polyfit 对其计算五次拟合多项式，存放在 p 中，再用 plot 求其在 x0 的 y0.

解题程序

x=[46;49;51;52;54;56;57;58;59;60;61;62;63;64;66;67;68;71;72;71];

y=[40;50;55;63;72;70;77;73;90;93;96;88;99;110;113;120;127;137;132;137

];

plot(x,y,'k','markersize',20);

axis([30 100 20 170]);

p=polyfit(x,y,5);

t=30:1:100;

s=polyval(p,t);

hold on

plot(t,s,'k-','linewidth',2)

grid

实验结论

p =

1.0e+04 *

-0.0000 0.0000 -0.0002 0.0141 -0.3963 4.4287

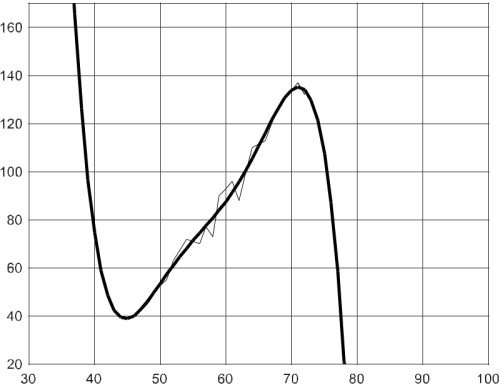
随着温度的上升，蟋蟀在单位时间内鸣叫的次数，先下降，再上升，然后接着下降，并在 70 时达到最高点，并且在 45~70 这一段曲线较为准确，当小于 45 时，可明显看出曲线上升的过于剧烈，与实际不符，若增测数据点，可能会有所改善。

分析总结

学会利用 matlab 用最小二乘法和不同次序的多项式对数据进行拟合拟合效果比较好

实验任务 2

① 实验问题：

（1）在下列数据中，W 表示一条鱼的重量，l 表示它的长度，使用最小二乘准则拟合模型 W=kl3

长度 l( 英寸 )	14.5	12.5	17.25	14.5	12.625	17.75	14.125	12.625
重量 w( 盎司 )	27	17	41	26	17	49	23	16

在下列数据中，g 表示一条鱼的身围，使用最小二乘准则拟合模型W=klg2

长度 l( 英寸 )	14.5	12.5	17.25	14.5	12.625	17.75	14.125	12.625
重量 w( 盎司 )	27	17	41	26	17	49	23	16
身围 g（英寸）	9.75	8.375	11.0	9.75	8.5	12.5	9.0	8.5

两个模型哪个拟合数据较好？为什么?

② 问题分析：

与上一题类似，该问题亦是一个典型的曲线拟合问题，故其要点应与上一题类似，即，如何找到一条曲线，使拟合出来的数据与实际数据的偏差较小。

③程序设计流程图：

（1）

l=[14.5 12.5 17.25 14.5 12.625 17.75 14.125 12.625];

w=[27 17 41 26 17 49 23 16];

a=0;b=0;

for i=1:8

a=a+l(i)^4;

b=b+l(i)*w(i);

end

A=a

B=b

q=inv(A)*B

for i=1:8

x(i)=q(1)*l(i)^3;

end

plot(l,w,'r*--',l,x,'b.--')

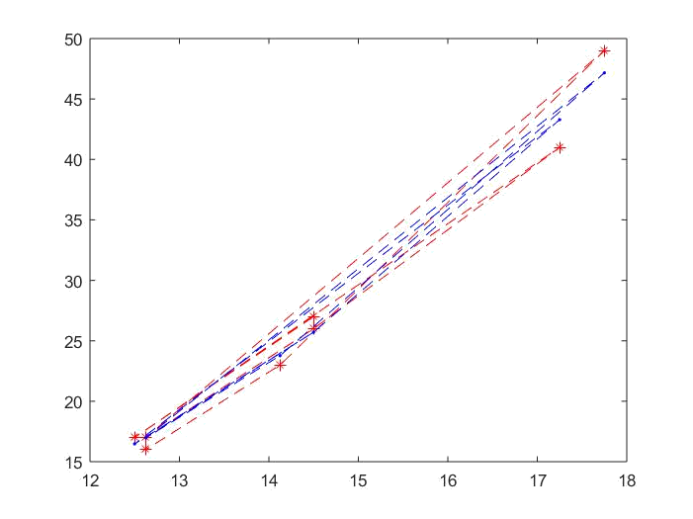
l=[14.5 12.5 17.25 14.5 12.625 17.75 14.125 12.625]; g=[9.75 8.375 11.0 9.75 8.5 12.5 9.0 8.5]; w=[27 17 41 26 17 49 23 16];

plot3(l,g,w,'k.','markersize',25)

axis([10 20 7 12 15 55])

a=l.*(g.^2)

b=inv(a*(a.'))*(a)*(w.')

x=10:0.1:20

y=7:0.1:13

[X,Y]=meshgrid(x,y)

Z=b*X.*Y.^2

surf(X,Y,Z)

shading flat

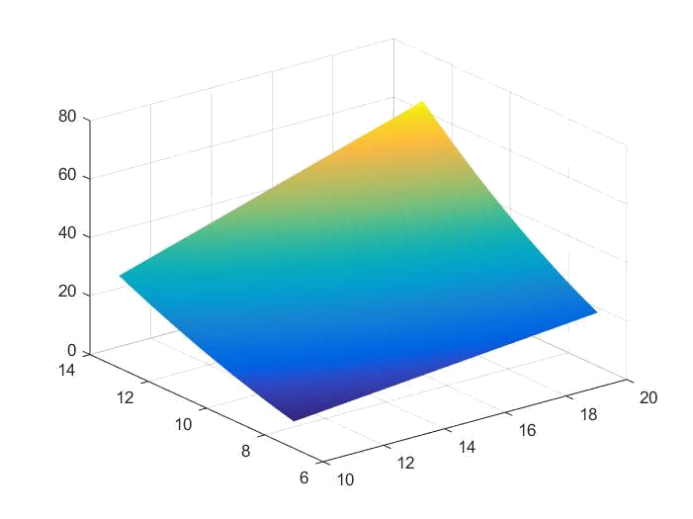
（3）2 中的拟合数据较好，因为鱼的重量不仅与其身长相关，亦与身围有密不可分的联系，综合考虑才能得到较好结果。④结果分析与结论：

从图像中可以看出，随着鱼身长与身围的增大，其质量在不断增加。总结与体会：通过这次拟合实验，我们发现，在做曲线拟合时，单方面考虑得出的结果往往具有较大局限性。多方综合考虑后，才能得到准确的结果。

5 总结与体会

通过这次实验，我对于最小二乘插值法有了更深刻的了解

实验任务 3

① 实验问题：有一形状较为复杂，但表面很光滑的曲面工件。通过科学手段，将其放置于某一空间坐标系下，测得曲面上若干个点的坐标如下：

坐标值	-5	-4	-3	-2	-1	1	2	3	4	5
-5	13.6	-8.2	-14.8	-6.6	1.4	-3.8	1.4	13.6	16.8	0
-4	-8.2	-15.8	-7.9	2.2	3.8	0.6	7.3	10.1	0	-16.8
-3	-14.8	-7.9	2.5	5.8	2.3	2.7	5.1	0	-10.1	-13.7
-2	-6.6	2.2	5.9	3	-0.3	1.9	0	-5.1	-7.3	-1.4
-1	1.4	3.8	2.3	-0.3	-0.9	0	-1.7	-2.7	-0.6	3.8
0	0	0	0	0	0	0	0	0	0	0
1	-3.8	0.6	2.7	1.7	0	0.9	0.3	-2.3	-3.8	-1.4
2	1.4	7.3	5.1	0	-1.7	0.3	-3.1	-5.8	-2.2	6.6
3	13.6	10.1	0	-5.1	-2.7	-2.3	-5.8	-2.5	7.9	14.8
4	16.8	0	-10.1	-7.3	-0.6	-3.8	-2.2	7.9	15.8	8.2
5	0	16.3	-13.6	-1.4	3.8	-1.4	6.6	14.8	8.2	-13.6

要求：

画出该曲面工件的图形

在已知相邻的横纵坐标之间分别插入三个分点，用 interp2 命令计算出所有点处的竖坐标，画出相应的插值曲面。

用不同方法求出该曲面工件表面积的近似值

② 问题分析：本题是一道典型的插值问题，第一问可以用指令迅速画出图形。第二问主要难点在于 interp2 命令的应用。第三问依据数学方法求解即可。

③ 程序设计流程图：

x=-5:1:5;

y=-5:1:5;

[xx,yy]=meshgrid(x,y);

zz=Sheet1;

figure(1);

mesh(xx,yy,zz);

figure(2)

xb=-5:0.25:5;

yb=-5:0.25:5;

[xxb,yyb]=meshgrid(xb,yb);

zzb=interp2(xx,yy,zz,xxb,yyb,'cubic');

mesh(xxb,yyb,zzb)

[Fx,Fy]=gradient(zz,0.001,0.001);

S=sqrt(1+Fx.^2+Fy.^2)*0.000001.*( ~isnan(zz) ) ;

sum(S(~isnan(S)))

④ 结果分析与结论：

原曲面：

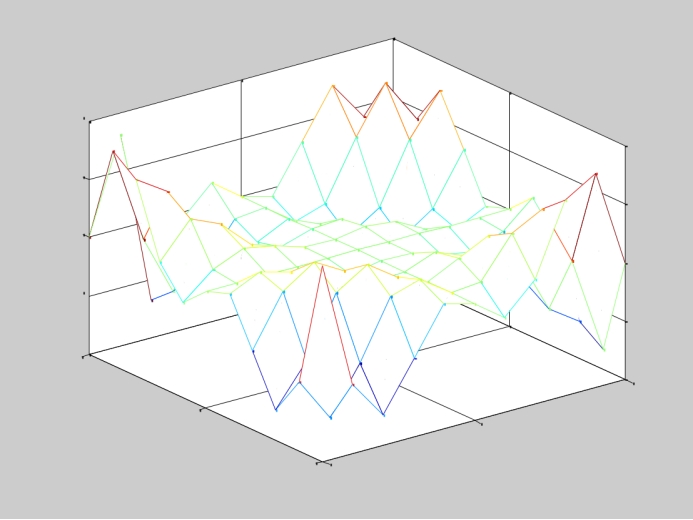
插值后的曲面：

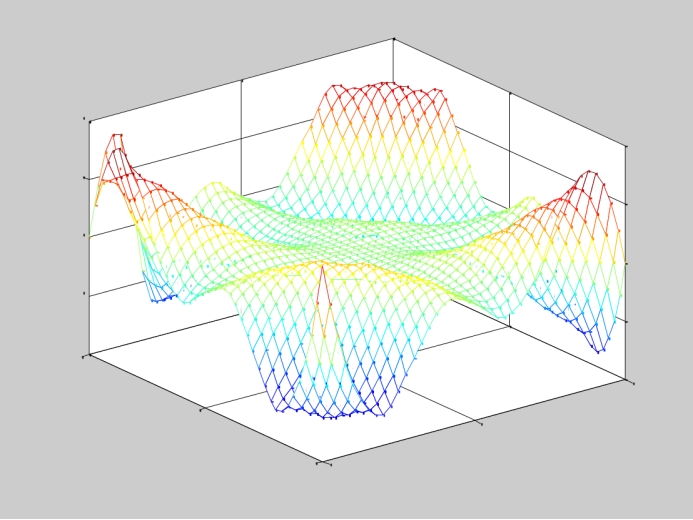
算得的曲面面积：

ans =0.7669

④ 总结与体会：通过本题，我们小组对二维插值问题有了一定的了解。

实验任务 4

① 实验问题：煤矿的储量估计，下表给出了某露天煤矿在平面矩形区域(1100mX700m)上，在纵横均匀的网格交点处测得的煤层厚度(单位:m)(由于客观原因，有些点无法测量煤层厚度，这里用/标出），其中的每个网格都为（100mX100m)的小矩形，试根据这些数据,来估算出该矩形区域煤矿的储藏量(体积）

	A	B	C	D	E	F	G	H	I	J	K
1	/	/	12.5	13.5	17.2	/	8.8	14.7	8.0	13.0	/
2	/	/	/	15.6	18.2	13	6.4	8.9	9.2	11.7	/
3	/	12	13.5	13.5	17.8	16.9	13.2	/	/	/	/
4	7.5	12.6	14.9	18.7	17.7	17.5	14.7	13	/	/	6.5
5	8.9	7.8	12.4	13.5	15.7	17.6	11.7	9.6	9.2	9.5	8.6
6	/	/	/	13.7	13.6	16.5	12.5	8.7	9.7	/	/
7	/	/	8.6	11.8	12.5	11.3	13.4	/	/	/	/

③ 问题分析：本题与之前的例题并无不同，关键在于如何化归。

③ 程序设计流程图：

x=0:100:1000;

y=0:100:600;

z=[14.2,14.1,12.5,13.5,17.2,12.9,8.8,14.7,8.0,13.0,10.3;

19.1,17.9,16.7,15.6,18.2,13,6.4,8.9,9.2,11.7,7.0;

12.4,12,13.5,13.5,17.8,16.9,13.2,16.5,17.1,17.7,18.3;

7.5,12.6,14.9,18.7,17.7,17.5,14.7,13,9.9,7.6,6.5;

8.9,7.8,12.4,13.5,15.7,17.6,11.7,9.6,9.2,9.5,8.6;

8.2,9.3,11.7,13.7,13.6,16.5,12.5,8.7,9.7,7.6,9.5;

8.1,10.8,8.6,11.8,12.5,11.3,13.4,11.0,8.4,5.0,0.88];

[x0,y0]=meshgrid(0:1:1000,0:1:600);

z1=interp2(x,y,z,x0,y0,'linear');

z2=interp2(x,y,z,x0,y0,'cubic');

z3=interp2(x,y,z,x0,y0,'spline');

%surf(x0,y0,z1)

%surf(x0,y0,z2)

surf(x0,y0,z3)

shading interp;

for i=1:601

for j=1:1001

%M(i,j)=z1(i,j);

%M(i,j)=z2(i,j);

M(i,j)=z3(i,j);

end

end

sum(sum(M))

④结果分析与结论：

第一种插值得到的曲面:

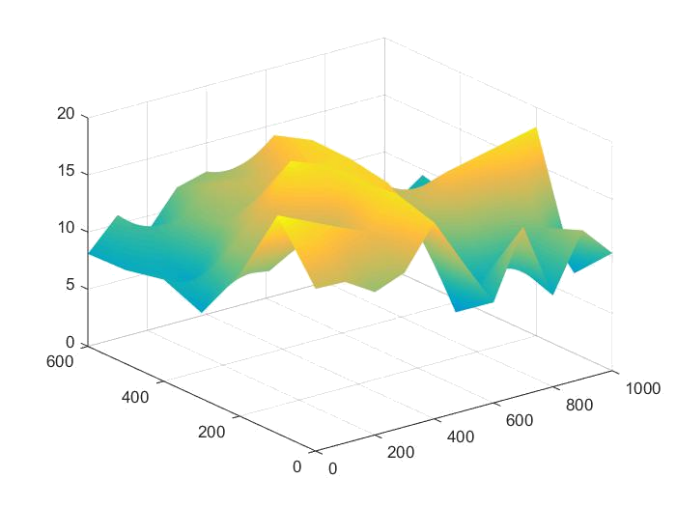
储量估计：

ans = 7.5956e+006

第二种插值得到的曲面：

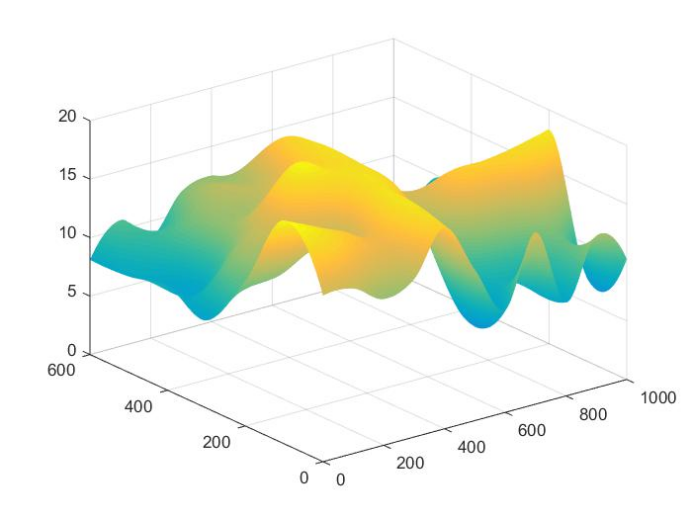
储量估计：

ans = 7.6190e+006

第三种插值值得到的曲面:

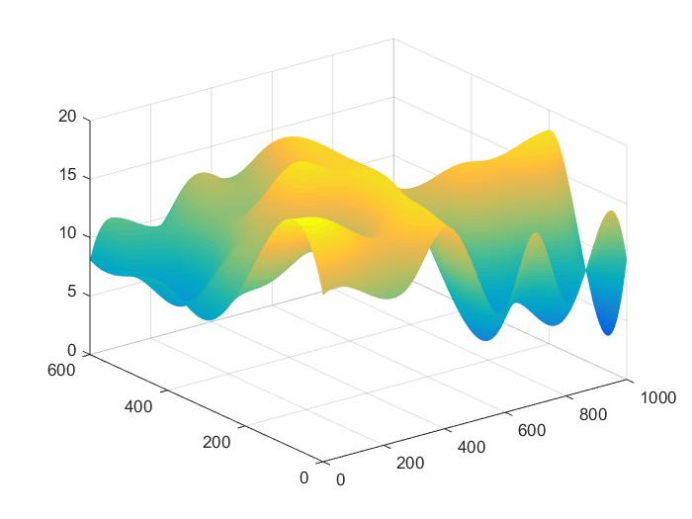
储量估计：

ans =7.6076e+006

5 总结与体会：本次实验，我们运用了三种不同的插值法来求解，实际所得结果相差不大，说明插值结果与实验比较吻合。

第一次任务

实验八 练习一 2.

实验八 练习一 5.

实验八 练习二 2.

实验九 3.

第二次任务

实验任务 1.

实验任务 2.

第三次任务

实验任务 1.

实验任务 2.

实验任务 3

实验任务4 练习2 1

第四次任务

实验任务 1

实验任务 2

第五次任务

实验任务 1

实验任务 2

实验任务 3

实验任务 4

实验八练习一 2.

实验八练习一 5.

实验八练习二 2.