文章导航
大二上大物实验下报告存档
一、 实验获得幅频曲线图
二、 设计一个利用本仪器测量微小质量变化的实验
(一) 实验原理
激光垂直入射相隔很近的两个光栅M，N．光栅N保持静止状态，光栅M粘贴于一个在与激光传播方向垂直的方向上做受迫微振动的音叉上．假设光栅M在该方向上的运动速度为v，则通过时间t，入射光的相位改变为
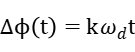
其中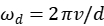
，d为光栅常数。
即对于分别从两个光栅出射的同一级衍射光，存在一个多普勒频移，大小为
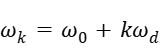
其中，
为M光栅出射的第k级衍射光的圆频率；
为N光栅出射的第k级衍射光的圆频率；k为衍射级次．
由于光的频率很高，用光电探测器无法测得，必须由衍射光相干叠加形成光拍．最终光电检测器检测到的光电流为
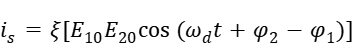
其中，
为光电转换常数；
，
分别为丽束相干光的能量；
，
分别为两束相干光的初相位．
拍频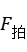
即为
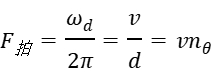
其中，v为M光栅移动速度；n。为光栅密度，等于100条／mm．
微弱振动的振幅为
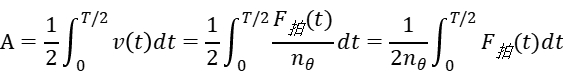
其中，T为音叉振动周期；
表示
时间
内的拍频波的个数．
由上式可知，只要测得拍频波的个数，就可得到微弱振动的振幅．
(二) 实验过程
\1. 音叉附着质量与音叉振幅关系定性研究
调节驱动频率使音叉谐振，将同一质量的铁丝放置于音叉上不同位置的小孔内，从而改变音叉附着质量．通过示波器上显示的拍频波个数计算出相应情况下的音叉振幅，拟合出音叉振幅大小与音叉附着质量位置关系曲线，如图1所示(A为音叉振幅大小，X为铁丝所在位置与音叉固定端的距离)．
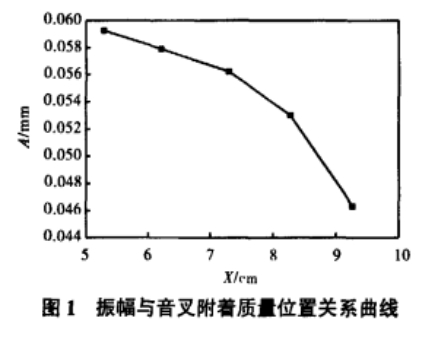
讨论：由图1可知，当音叉谐振时，改变音又的附着质量可以很明显地改变音叉的振幅，且附加的铁丝距离音叉固定端越远，音叉附着质量越大，音叉的振幅越小，说明音叉附着质量与音叉振幅存在某种反比关系．
\2. 音叉附着质量与音叉振幅关系定量研究
调节驱动频率使音叉谐振，用
1／10 000天平测量出质量范围在0．03～0．09 g之间的8段不同质量的铁丝，将它们分别放置于音叉上的同一位置(与音叉固定端距离为5．21 cm)，通过示波器上显示的拍频波个数计算出相应情况下的音叉振幅，得到音又振幅大小与铁丝质量(附着质量)大小的拟合曲线如图2所示A为音叉振幅，m为铁丝质量)．
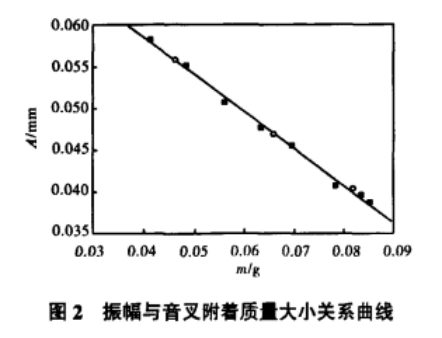
讨论：由图2可以看出(实心黑点所在位置为实验采集数据)，在音叉谐振的状态下，在音叉的同一位置附着不同质量的物体，改变音叉的附着质量，音叉振幅随附着铁丝质量的增大而减小，且附着物体质量
大小和音叉振幅大小近似存在线性关系，此线性函数关系为：
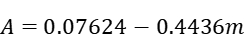
其中，A为音叉振幅，mm；m为微小物体质量，g．
对于质量位于本实验所采用的质量区间内的微小物体，都可以通过双光栅微弱振动实验测量出振幅，再利用上式计算出质量大小．而对于任意双光栅仪器，也可以采用上述的方法，测量微小物体质量大小．
——摘自《利用双光栅开展设计性实验的探讨》易静
中图分类号：TH744 文献标识码A 文章编号：1006．6853(2009)04—0314—03
三、 查阅“光栅尺”，也称莫尔条纹在工业中是如何进行微小量的测量和控制的。
(一) 莫尔条纹
以透射光栅为例，当指示光栅上的线纹和标尺光栅上的线纹之间形成一个小角度θ，并且两个光栅尺刻面相对平行放置时，在光源的照射下，位于几乎垂直的栅纹上，形成明暗相间的条纹。这种条纹称为“莫尔条纹” (右图所示)。严格地说，莫尔条纹排列的方向是与两片光栅线纹夹角的平分线相垂直。莫尔条纹中两条亮纹或两条暗纹之间的距离称为莫尔条纹的宽度，以W表示。
W=ω /2* sin（θ /2）=ω /θ 。
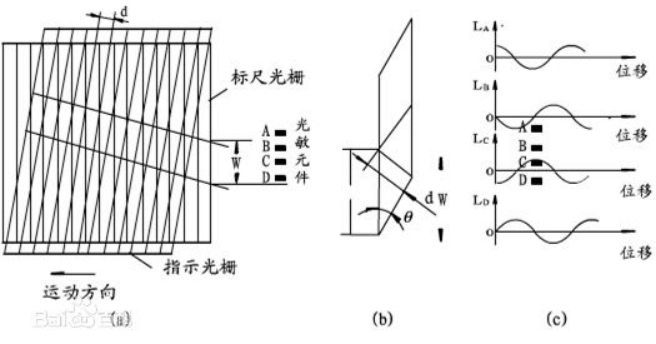
莫尔条纹
(三) 莫尔条纹具有以下特征：
(1)莫尔条纹的变化规律
两片光栅相对移过一个栅距，莫尔条纹移过一个条纹距离。由于光的衍射与干涉作用，莫尔条纹的变化规律近似正(余)弦函数，变化周期数与光栅相对位移的栅距数同步。
(2)放大作用
在两光栅栅线夹角较小的情况下，莫尔条纹宽度W和光栅栅距ω、栅线角θ之间有下列关系。式中，θ的单位为rad，W的单位为mm。由于倾角很小，sinθ很小，则
W=ω /θ
若ω =0．01mm，θ=0.01rad，则上式可得W=1，即光栅放大了100倍。
(3)均化误差作用
莫尔条纹是由若干光栅条纹共用形成，例如每毫米100线的光栅，10mm宽度的莫尔条纹就有1000条线纹，这样栅距之间的相邻误差就被平均化了，消除了由于栅距不均匀、断裂等造成的误差。
(四) 检测与数据处理
电子细分与判向法
光栅测量位移的实质是以光栅栅距为一把标准尺子对位称量进行测量。高分辨率的光栅尺一般造价较贵，且制造困难。为了提高系统分辨率，需要对莫尔条纹进行细分，光栅尺传感器系统多采用电子细分方法。当两块光栅以微小倾角重叠时，在与光栅刻线大致垂直的方向上就会产生莫尔条纹，随着光栅的移动，莫尔条纹也随之上下移动。这样就把对光栅栅距的测量转换为对莫尔条纹个数的测量。
在一个莫尔条纹宽度内，按照一定间隔放置4个光电器件就能实现电子细分与判向功能。例如，栅线为50线对/mm的光栅尺，其光栅栅距为0.02mm，若采用四细分后便可得到分辨率为5μm的计数脉冲，这在工业普通测控中已达到了很高精度。由于位移是一个矢量，即要检测其大小，又要检测其方向，因此至少需要两路相位不同的光电信号。为了消除共模干扰、直流分量和偶次谐波，通常采用由低漂移运放构成的差分放大器。由4个光敏器件获得的4路光电信号分别送到2只差分放大器输入端，从差分放大器输出的两路信号其相位差为π/2，为得到判向和计数脉冲，需对这两路信号进行整形，首先把它们整形为占空比为1：1的方波。然后，通过对方波的相位进行判别比较，就可以等到光栅尺的移动方向。通过对方波脉冲进行计数，可以得到光栅尺的位移和速度
四、 查阅利用测量固体金属的固有频率，如何计算出该金属的杨氏模量。
对于长度L≫直径d、两段自由地做微小横振动的均匀细棒，其振动满足方程
+
=0
式中，ρ为棒的密度，S为棒的截面积，J=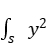
dS称为惯量矩（取决于截面的形状），E为杨氏模量，y为棒振动的位移，x为位置坐标，t为时间变量。
用分离变量法解方程，令y（x，t）=X(t)T(t)代入方程，有
=
解得该振动方程的通解为
y（x，t）=（B1chKx+B2shKx+B3cosKx+B4sinKx）Acos（ωt+φ）
式中
ω =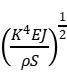 
称为频率公式。频率公式对任意形状的截面、不同边界条件的试样都是成立的。我们只要用特定的边界条件定出常数K，带入特定截面的惯量矩J，就可以得到具体条件下的计算公式。如果悬线悬挂在试样的节点（处在共振状态的棒中，位移恒为零的位置）附近，则棒的两端均处于自由状态。此时其边界条件为自由端横向作用力F和弯矩M均为零，即
F=-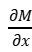
=- EJ
=0
弯矩
M=EJ
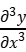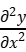=0
故有
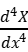|x=0=0 
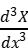|x=l=0 
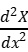|x=0=0 
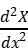|x=l=0
将通解代入边界条件，可以得到cosKl*chKl=1，可用数值解法求得本征值K和棒长l应满足Kl=0，4.730，7.853，10.996，14.137，。。。
一般将K1l=4.730所对应的频率称为基频频率。
试样在做基频振动时，存在两个节点，它们的位置距离端面为0.224l和0.776l处。将第一本征值K1=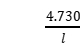
代入频率表达式，得到自由振动的固有圆频率（基频）
ω =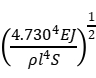 
解出杨氏模量
E=7.8870*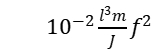
对于直径为d的圆形棒，惯量矩
J=
dS=S(
=
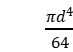
代入上式可得
E=1.6067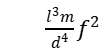
式中，l为棒长，d为棒的直径，m为棒的质量，f为试样共振频率。在国际单位制中杨氏模量E的单位为N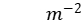
.
实际上，E还和试样的直径与长度之比d/l的大小有关，所以乘以一个修正因子R，则有
E=1.6067R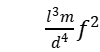
当l≫d时，R≈1；当l≫d不成立时，圆棒的R可查表
试样R与d/l的关系
| d/l | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 |
|---|---|---|---|---|---|---|
| R | 1.001 | 1.002 | 1.005 | 1.008 | 1.014 | 1.019 |
当外力频率达到共振频率ωr时，另一悬线处会接收到最大振幅，而固有频率与共振频率之间的关系为fr=
=
，
为阻尼系数。对于一般的金属材料，β的最大值只有ω的1%左右，所以可用fr代替f计算。
五、 利用本实验仪器，还可以进行哪方面的研究？
还可以测量力、光、电学方面的微小变化量，监测分析系统中的微小故障，如用来研究航空航天、船舶、兵器军工、冶金、化工、机械制造、电力、供水等行业设备管理工作的故障诊断。
(1)在桥梁安全监测中的应用
目前, 应用光纤光栅传感器最多的领域当数桥梁的安全监测。斜拉桥斜拉索、悬索桥主缆及吊杆和系杆拱桥系杆等是这些桥梁体系的关键受力构件,其他土木工程结构的预应力锚固体系,如结构加固采用的锚索、锚杆也是关键的受力构件。上述受力构件的受力大小及分布变化最直接地反映结构的健康状况,因此对这些构件的受力状况监测及在此基础上的安全分析评估具有重大意义。
(2)在水位遥测中的应用
在光纤光栅技术平台上研制出的高精度光学水位传感器专门用于江河、湖泊以及排污系统水位的测量。传感器的精度可以到达±0.1%F·S。光纤安装在传感器内部，由于光纤纤芯折射率的周期性变化形成了FBG，并反射符合布拉格条件的某一波长的光信号。当FBG与弹性膜片或其它设备连接在一起时，水位的变化会拉伸或压缩FBG。而且，反射波长会随着折射率周期性变化而发生变化。那么，根据反射波长的偏移就可以监测出水位的变化。
六、 普通光栅与相位光栅的区别
普通光栅：由大量等宽等间距的平行狭缝构成的光学器件称为光栅(grating)。一般常用的光栅是在玻璃片上刻出大量平行刻痕制成，刻痕为不透光部分，两刻痕之间的光滑部分可以透光，相当于一狭缝。精制的光栅，在1cm宽度内刻有几千条乃至上万条刻痕。这种利用透射光衍射的光栅称为透射光栅，还有利用两刻痕间的反射光衍射的光栅，如在镀有金属层的表面上刻出许多平行刻痕，两刻痕间的光滑金属面可以反射光，这种光栅称为反射光栅。
相位光栅：所谓的位相材料是指那些只有空间位相结构，而透明度一样的透明材料，如生物切片、油膜、热塑以及声光偏转池等，他们只改变入射光的相位，而不影响其振幅。位相光栅就是用这样的材料制作的光栅。
区别：普通光栅会同时改变入射光的振幅与相位，而相位光栅只改变入射光的相位。
