数据结构实验3——树的遍历操作及基于霍夫曼树的编码/译码

全文共: 2.4k字   |   阅读时长: 11分
知识整理本科课程大二
  阅读

文章导航

大二上数据结构实验1内容，使用C语言实现树的遍历操作及基于霍夫曼树的编码/译码

一、实验题目和要求

实验题目：树的遍历操作及基于霍夫曼树的编码/译码 （一）实验目的：掌握结构体、指针及二叉树的生成、遍历等操作，掌握霍夫曼编码/译码的原理。 （二）基本要求：熟练掌握树的操作。 （三）内容提要： 1）通过键盘输入一段字符(长度>=20)，构建霍夫曼树； 2）根据该树求每个字符的编码，并对该段字符串进行编码； 3）将得到的编码进行译码； 4）基于该霍夫曼树，实现非递归的先序遍历算法，输出该树所有的节点、节点的权值、节点的度和节点所在的层数； 5）基于该霍夫曼树，实现基于队列的层序遍历算法，输出该树所有的节点、节点的权值、节点的度和节点所在的层数。

注：在实现时要求霍夫曼树的左右孩子的大小关系满足，左孩子节点权值小于右孩子节点权值。

二、按不同功能分析各程序模块

(一)包含库函数、定义常量、变量类型

1
2
3
4
5
6
7
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#define MAXSTRLEN 256//输入字符串的最大长度
#define STACK_INIT_SIZE 100//栈的储存空间初始分配量
#define STACKINCREMENT 10//栈的存储空间分配增量

(二)构建哈夫曼树、栈、队列的结构、操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
typedef struct HTNode//哈夫曼树
{
    unsigned int weight;
    unsigned int parent, lchild,rchild;
    struct HTNode *Parent,*Lchild,*Rchild;
    unsigned int degree;
    unsigned int depth;
}HTNode,*HuffmanTree;
typedef char **HuffmanCode;//哈夫曼编码表
typedef struct//栈
{
    HuffmanTree *base;
    HuffmanTree *top;
    int stacksize;
}SqStack;
int InitStack(SqStack&S)//构造空栈
{
    S.base=(HuffmanTree*)malloc(STACK_INIT_SIZE*sizeof(HuffmanTree));
    if(!S.base)exit(-1);
    S.top=S.base;
    S.stacksize=STACK_INIT_SIZE;
    return 1;
}
int GetTop(SqStack S,HuffmanTree&e)//读取栈顶元素
{
    if(S.top==S.base)return 0;
    e = *(S.top-1);
    return 1;
}
int Push(SqStack&S,HuffmanTree e)//进栈
{
    if(S.top-S.base>=S.stacksize)
    {
        S.base=(HuffmanTree*)realloc(S.base,(S.stacksize+STACKINCREMENT)*sizeof(HuffmanTree));
        if(!S.base)exit(-1);
        S.top=S.base+S.stacksize;
        S.stacksize+=STACKINCREMENT;
    }
    *S.top++=e;
    return 1;
}
int Pop(SqStack&S,HuffmanTree &e)//出栈
{
    if(S.top==S.base)return 0;
    e=*--S.top;
    return 1;
}
int StackEmpty(SqStack S)//判断为空栈
{
    if(S.top==S.base) return 1;
    else return 0;
}
typedef struct QNode//队列
{
    HuffmanTree data;
    struct QNode *next;
}QNode,*QueuePtr;
typedef struct//队列头尾指针
{
    QueuePtr Front;
    QueuePtr Rear;
}LinkQueue;
int InitQueue(LinkQueue &Q)//构造空队列
{
    Q.Front=Q.Rear=(QueuePtr)malloc(sizeof(QNode));
    if(!Q.Front) exit(-1);
    Q.Front->next=NULL;
    return 1;
}
int EnQueue(LinkQueue &Q,HuffmanTree e)//入队
{
    QueuePtr p;
    p=(QueuePtr)malloc(sizeof(QNode));
    if(!p) exit(-1);
    p->data=e;p->next=NULL;
    Q.Rear->next=p;
    Q.Rear=p;
    return 1;
}
int DeQueue(LinkQueue &Q,HuffmanTree &e)//出队
{
    QueuePtr p;
    if(Q.Front==Q.Rear)return 1;
    p=Q.Front->next;
    e=p->data;
    Q.Front->next=p->next;
    if(Q.Rear==p)Q.Rear=Q.Front;
    free(p);
    return 1;
}
int QueueEmpty(LinkQueue Q)//判断队列是否为空
{
    if(Q.Front==Q.Rear) return 1;
    else return  0;
}

(三)构建哈夫曼树、求编码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
void Select(HuffmanTree HT,int n,int *s1,int *s2)//选择两个最小结点
{
	int i;
	int min1,min2;
	int S1,S2;
	min1=INT_MAX;
	min2=INT_MAX;
	for(i=1;i<=n;i++)
	if(HT[i].parent==0){
		if(HT[i].weight<=min1){
			min1=HT[i].weight;
			S1=i;
		}
	}
	for(i=1;i<=n;i++)
	if(HT[i].parent==0&&i!=S1){
		if(HT[i].weight<=min2){
			min2=HT[i].weight;
			S2=i;

		}
	}
	if(min2<=min1){
		int temp;
		temp=S1;
		S1=S2;
		S2=temp;
	}
	*s1=S1;
	*s2=S2;

}
void HuffmanCoding(HuffmanTree &HT,HuffmanCode &HC,int *w,int n)//构建哈夫曼树，求哈夫曼编码
{
	if(n<=1)
    return;
    int m;
    m=2*n-1;
    HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode));
    HuffmanTree p;
    int i;
    int s1,s2;
    for(p=HT+1,i=1;i<=n;++i,++p,++w)
    {
    	*p={*w,0,0,0,NULL,NULL,NULL,0,0};
	}
	for(;i<=m;++i,++p)
	{
		*p={0,0,0,0,NULL,NULL,NULL,0,0};
	}
	for(i=n+1;i<=m;++i)
	{
		Select(HT,i-1,&s1,&s2);
		HT[s1].parent=i;
		HT[s2].parent=i;
		HT[i].lchild=s1;
		HT[i].rchild=s2;
		HT[i].weight=HT[s1].weight+HT[s2].weight;
        HT[s1].Parent=&HT[i];
        HT[s2].Parent=&HT[i];
        HT[i].Lchild=&HT[s1];
        HT[i].Rchild=&HT[s2];
	}//构建霍夫曼树
	HC=(HuffmanCode)malloc((n+1)*sizeof(char*));
	char cd[n];
	cd[n-1]='\0';
	int start,c,f;
	for(i=1;i<=n;++i)
	{
		start=n-1;
		for(c=i,f=HT[i].parent;f!=0;c=f,f=HT[f].parent)
		{
			if(HT[f].lchild==c)
			{
				cd[--start]='0';
			}
			else
			cd[--start]='1';
		}
		HC[i]=(char*)malloc((n-start)*sizeof(char));
		strcpy(HC[i],&cd[start]);
	}//求哈夫曼编码
}

(四)编码、解码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int getcode(HuffmanCode &code,char* str,HuffmanCode HC,char* word)//编码
{
    int i,j;
    printf("\n编得的码为：");
    for(i=0;str[i]!='\0';i++)
    {
        j=0;
        while(str[i]!=word[j])
            j++;
        //printf("%s",HC[j+1]);
        code[i]=HC[j+1];
        printf("%s",code[i]);
    }
    code[i]=NULL;
    return 1;
}
int encode(HuffmanCode code,HuffmanCode HC,char* word)//解码
{
    int i,j;
    printf("\n解得的码为：");
    for(i=0;code[i]!=NULL;i++)
    {
        j=1;
        while(strcmp(code[i],HC[j]))
            j++;
        //printf("%d",j);
        printf("%c",word[j-1]);
    }
    return 1;
}

(五)两种遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
void Depth(HuffmanTree T)//求哈夫曼树节点的深度（所在层数）
{
    int i=1;
    HuffmanTree p;
    p=T;
    while(p->Parent!=NULL)
    {
        p=p->Parent;i++;
    }
    T->depth=i;
}
void Degree(HuffmanTree T)//求哈夫曼树节点的度
{
    if(T->lchild&&T->rchild) T->degree=2;
    else if(!T->lchild&&!T->rchild) T->degree=0;
    else T->degree=1;
}
void Visit(HuffmanTree p,HuffmanCode HC,char *word,int n)//输出该节点、节点的权值、节点的度和节点所在的层数。
{
    Depth(p);
    Degree(p);
    int i,start;
    HuffmanTree f,c;
    char a;
    char *b;
    if(p->degree==0)
    {
        b=(char*)malloc((n*sizeof(char)));
        b[n-1]='\0';
        start=n-1;
        for(c=p,f=p->Parent;f!=NULL;c=f,f=f->Parent)
		{
			if(f->Lchild==c)
				b[--start]='0';
			else
			    b[--start]='1';
		}
        i=1;
        while(strcmp(HC[i],&b[start])){i++;}
        //printf("%d ",i);
        a=word[i-1];
        printf("");
    	printf("存的是字符%c ",a);
	}
	else
        printf("存的不是字符 ");
    printf("权值：%d 度：%d 层数：%d\n",p->weight,p->degree,p->depth);
}
int PreTraverse(HuffmanTree HT,HuffmanCode HC,int n,char *word)//先序遍历
{
    int m;
    m=2*n-1;
    HuffmanTree p;
    p=HT;
    SqStack s;
    InitStack(s);
    Push(s,p);
    while(!StackEmpty(s))
    {
        Pop(s,p);
        Visit(p,HC,word,n);
        if(p->Rchild)
            Push(s,p->Rchild);
        if(p->Lchild)
            Push(s,p->Lchild);
    }
    return 1;
}
int LevelTraverse(HuffmanTree HT,HuffmanCode HC,int n,char *word)//层序遍历
{
    int m;
    m=2*n-1;
    HuffmanTree p;
    LinkQueue Q;
    InitQueue(Q);
    p=HT;
    Visit(p,HC,word,n);
    while(p||!QueueEmpty(Q))
    {
        if(p->Lchild)
        {
            Visit(p->Lchild,HC,word,n);
            EnQueue(Q,p->Lchild);
        }
        if(p->Rchild)
        {
            Visit(p->Rchild,HC,word,n);
            EnQueue(Q,p->Rchild);
        }
        DeQueue(Q,p);
    }
    return 1;
}

(六)主函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
int main()
{
    HuffmanTree HT;
    HuffmanCode HC;
    char str[MAXSTRLEN];
    printf("请输入一串长度大于20字符\n");
    gets(str);
    int num;            //不同字符种数
    char *word;         //所有出现的字符
    int *weight;        //存放字符权值的数组
    int a[128]={0};
    int i,j;
    for( i=0;str[i]!='\0';i++ )
    {
         if ( str[i] < 127 )
             a[str[i]]++;
         else
             a[127]++;
    }
    for( i=0,num=0;i<128;i++ )
        if ( a[i] > 0 )
            num++;
    word=(char*)malloc(num*sizeof(char*));
    weight=(int*)malloc(num*sizeof(int*));
    for( i=0,j=0;i<128;i++ )
        if ( a[i] > 0 )
        {
            word[j]=(char)i;
            weight[j]=a[i];
            j++;
        }
    word[j]='\0';
    printf("总共的字符种类：%s",word);
    printf("\n每个字符出现的次数：");
    for(i=0;i<num;i++)
    {
        printf("%c：%d ",word[i],weight[i]);
    }
    printf("\n");
    HuffmanCoding(HT,HC,weight,num);
    printf("对应的哈夫曼编码为：");
    for(i=1;i<num+1;i++)
    {
        printf("%c：%s ",word[i-1],HC[i]);
    }
    HuffmanCode code;
    code=(HuffmanCode)malloc((num+1)*sizeof(char*));
    getcode(code,str,HC,word);
    encode(code,HC,word);
    printf("\n");
    HuffmanTree T;
    T=&HT[num*2-1];
    printf("先序遍历结果为：\n");
    PreTraverse(T,HC,num,word);
    printf("层序遍历结果为：\n");
    LevelTraverse(T,HC,num,word);
    printf("\n");
    return 0;
}

三、思路分析

  1. 在本实验中，使用getchar（）从键盘输入一个字符串，建立一个长度为128的数组（用于对应ASCII码表），用于存储记录每个字符出现的次数，利用循环即可得到，用word数组存储所有出现的字符，并且将其一一对应到存储节点权值的数组weight中
  2. 利用子函数HuffmanCoding（）构建哈夫曼树。先将n个节点分别对应到n个字符上，令其权值为字符出现的次数。用select（）函数每次取出权值最小的两个节点，将其权值相加，作为父节点的权值，小的为左子节点，大的为右子节点。求编码时，由叶子节点向上回溯，如果为左子节点，就为0，否则为1。编码为其倒序输出。
  3. 将求得的编码和字符一一对应即可得到编码与解码
  4. 先序遍历时，先将根节点压栈，当栈非空时，执行循环：弹出p，访问p指针指向的节点，如果p节点左孩子指针非空，将左孩子压栈，如何p节点右孩子指针非空，将右孩子压栈。即可实现非递归的先序遍历。
  5. 层序遍历时，先将根节点入队，访问根节点，当队列非空或p指针非空时，执行循环：如果p的左孩子指针非空，将p的左孩子入队，如果p的右孩子指针非空，将p的右孩子入队，将队列尾节点退队。即可实现非递归的层序遍历。 Ps：select函数：用两个循环分别找到权值数组中最小的两个值，用一个判断保证s1<s2。 visit函数：用一个判断保证当节点度数为0是为字符，依据其编码确定是哪个字符；否则不是字符。再输出节点的度数、深度、权值。

四、运行结果分析

随便输入一组字符运行结果如下：

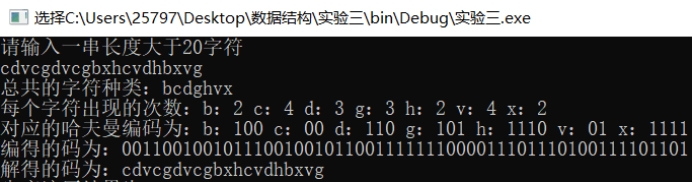
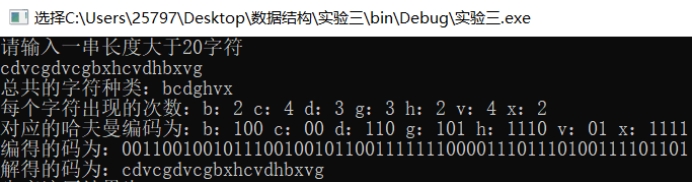
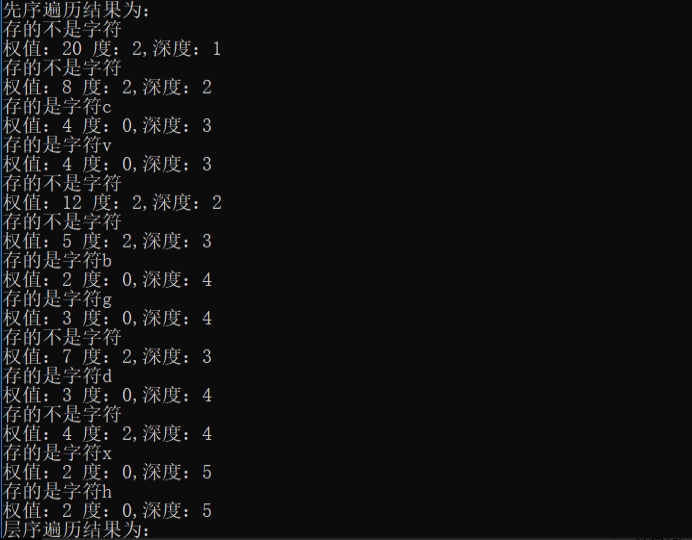
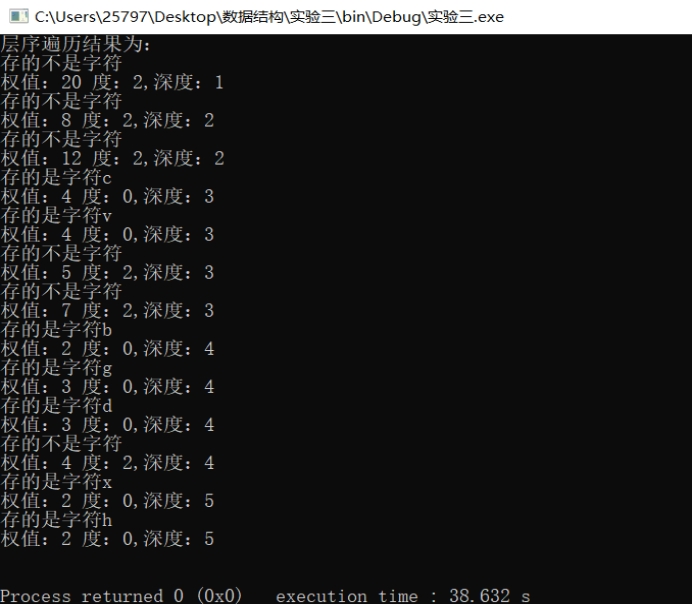
根据画图分析，运行结果正确。

本站总访问量次 | 您是第位访客