2018-12-01

数据结构实验4——无向图最短路径搜索

全文共: 1.3k字 | 阅读时长: 5分

阅读

文章导航

大二上数据结构实验1内容，使用C语言实现无向图最短路径搜索

一、实验题目和要求

实验题目：无向图最短路径搜索 （一）实验目的：掌握 Dijkstra 算法的原理。 （二）基本要求：熟练掌握图的操作。 （三）内容提要： 1）下图为校内知名建筑物示意平面图（其中“传送门”用于增加网络复杂度），以边表示建筑物间的路径，各条路径上方的数字表示路径长度。 2）针对该图进行构建数据结构和算法，通过键盘输入任意两建筑物的名称，可查询建筑物间的最短路径长度，并输出最短路径。注：1）用无向网表示校园内的各建筑的平面图，将平面图看作一张带权无向图，为此图选择适当的数据结构。 2）Dijkstra 算法是典型的单源最短路径算法，用于计算节点间的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。本次实验采用此算法求图中两点间的最短路径。

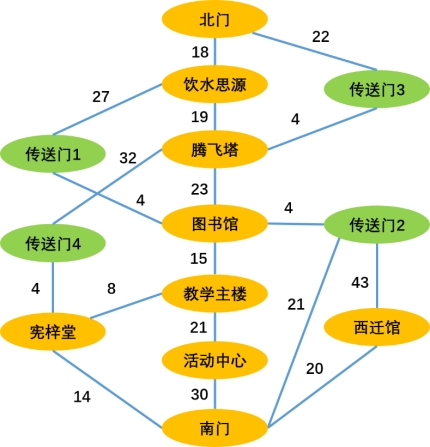
【输入样例】北门南门

【输出样例】 74 北门->传送门3->腾飞塔->图书馆->传送门2->南门

二、按不同功能分析各程序模块

(一)包含库函数、定义常量、变量类型

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define FALSE 0
#define TRUE 1
#define ERROR 0
#define OK 1
#define OVERFLOW -1
#define MAX_CHAR_LEN 20
#define INFINITY 1000 //最大值
#define MAX_VERTEX_NUM 13//最大顶点个数

(二)图的存储结构定义

typedef enum {DG,DN,UNG,UDN} GraphKind;
typedef int ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef struct
{
    char * vex[MAX_VERTEX_NUM];//顶点向量
    AdjMatrix arcs;         //邻接矩阵
    int vexnum,arcnum;      //当前顶点数，弧数
    GraphKind kind;         //图的种类
}MGraph;

(三)迪杰斯特拉算法求最短路径

void ShortestPath_DIJ(MGraph G,int v0, int vm,int P[MAX_VERTEX_NUM][MAX_VERTEX_NUM],int D[])
{
    int v,w,min,i,j;
    int Final[MAX_VERTEX_NUM];
    for(v=0;v<G.vexnum;++v)
    {
        Final[v]=FALSE;D[v]=G.arcs[v0][v];
        for(w=0;w<G.vexnum;++w) P[v][w]=FALSE;
        if(D[v]<INFINITY){P[v][v0]=TRUE;P[v][v]=TRUE;}
    }
    D[v0]=0;Final[v0]=TRUE;
    //for(i=1;i<G.vexnum;++i)
    while(Final[vm]==0)
    {
        min=INFINITY;
        for(w=0;w<G.vexnum;++w)
        {
            if(!Final[w])
                if(D[w]<min){v=w;min=D[w];}
        }
        Final[v]=TRUE;
        for(w=0;w<G.vexnum;++w)
        {
            if(!Final[w]&&(min+G.arcs[v][w]<D[w]))
            {
               D[w]=min+G.arcs[v][w];
               for(j=0;j<G.vexnum;++j)
               {
                  P[w][j]=P[v][j];
               }//P[w]=P[v];
               P[w][w]=TRUE;
            }
        }
    }
}

(四)主函数（输入查找的起点终点，输出最短路径）

int main()
{
    char x1[MAX_CHAR_LEN],x2[MAX_CHAR_LEN];
    scanf("%s %s",x1,x2);
    MGraph G;
    G.vex[0]="北门";
    G.vex[1]="饮水思源";  G.vex[2]="腾飞塔";  G.vex[3]="图书馆";  G.vex[4]="教学主楼";
    G.vex[5]="活动中心";  G.vex[6]="南门";    G.vex[7]="西迁馆";  G.vex[8]="传送门2";
    G.vex[9]="传送门3";   G.vex[10]="传送门1";G.vex[11]="传送门4";G.vex[12]="宪梓堂";
    G.vexnum=MAX_VERTEX_NUM;
    int i,j;
    for(i=0;i<MAX_VERTEX_NUM;i++)
        for(j=0;j<MAX_VERTEX_NUM;j++) G.arcs[i][j]=INFINITY;
    G.arcs[0][1]=18;G.arcs[1][2]=19;G.arcs[2][3]=23;G.arcs[3][4]=15;G.arcs[4][5]=21;G.arcs[5][6]=30;
    G.arcs[6][8]=21;G.arcs[3][8]=4;G.arcs[7][8]=43;G.arcs[6][7]=20;G.arcs[6][12]=14;G.arcs[4][12]=8;
    G.arcs[11][12]=4;G.arcs[3][10]=4;G.arcs[1][10]=27;G.arcs[0][9]=22;G.arcs[2][9]=4;G.arcs[2][11]=32;
    for(i=0;i<MAX_VERTEX_NUM;i++)
        for(j=i+1;j<MAX_VERTEX_NUM;j++)
            if(G.arcs[i][j]!=INFINITY) G.arcs[j][i]=G.arcs[i][j];
    int v0,vm;
    for(v0=0;v0<MAX_VERTEX_NUM;v0++)
        if(strcmp(G.vex[v0],x1)==0) break;
    for(vm=0;vm<MAX_VERTEX_NUM;vm++)
        if(strcmp(G.vex[vm],x2)==0) break;
    int D[MAX_VERTEX_NUM];
    for(i=0;i<MAX_VERTEX_NUM;i++) D[i]=INFINITY;
    int P[13][13];
    ShortestPath_DIJ(G,v0,vm,P,D);
    printf("%d\n",D[vm]);
    char *p;
    int m;
    m=v0;
    printf("%s->",G.vex[m]);
    P[vm][m]=0;
    while(m!=vm)
    {
    for(i=0;i<13;i++)
    if(G.arcs[m][i]!=INFINITY&&P[vm][i]==TRUE)
    {
    	printf("%s",G.vex[i]);
		if(i!=vm) printf("->");break;
	}
	m=i;P[vm][i]=FALSE;
    }
    return 0;
}

三、思路分析

用邻接矩阵存储图的边信息
输入起点终点，判断它们的编号，传入求路线的函数中
用dijkstra算法求从起点到任意一点的最短路径——一种优化方法，只求到所输入的终点为止——一次循环得出一个节点的最短路径，更新最短路径长度数组（确定为最短的节点对应final数组为true），并更新记录经过节点的矩阵
输出终点对应的路径长度，用循环依次筛选对应路径（该节点与当前位置相邻且对应于经过节点矩阵那行的对应位置为true），输出路径上的节点。循环完一次后当前位置进1，且把经过的路径对应矩阵中元素置为false（防止回溯）

四、运行结果分析

题目要求用例：

自己测试的用例：

根据画图分析，运行结果正确。