2019-06-05

概率统计上机题

全文共: 3.2k字 | 阅读时长: 12分

阅读

文章导航

大二下概率统计上机实验报告（大作业）

概率统计上机实验题

第一题

一、对二项分布事件概率的精确计算与用泊松分布和中心极限定理的近似计算进行对比。

（a） p变化，n固定，进行比较。（b）n变化,p固定，进行比较。

clear

n=100;

x=1:n;

y=1:0.1:n;

p=0.2;

p1=binopdf(x,n,p);

plot(x,p1,'r-','LineWidth',2)%画二项分布的精确分布曲线

hold on

lambta=n*p;

for i=1:n %求泊松分布的近似概率分布

 p2(i)=lambta^i*exp(-lambta)/factorial(i);

end

plot(x,p2,'b-','LineWidth',2)%画泊松分布的近似分布曲线

hold on

p3=normpdf(y,lambta,sqrt(lambta)*(1-p));

plot(y,p3,'g-','LineWidth',2)%画正态分布的近似分布曲线

title('n=100,p=0.2时三种情况下的概率曲线')

（a）

Ps：标准是红色（最细）、泊松是蓝色（最粗）、正态是绿色（中等粗细）

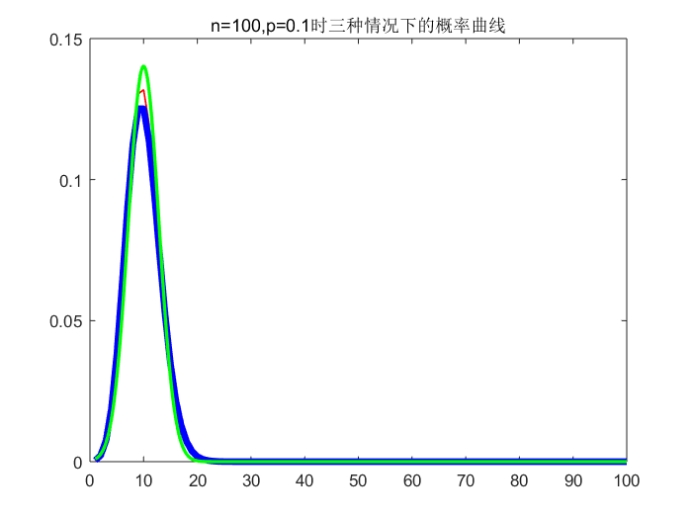
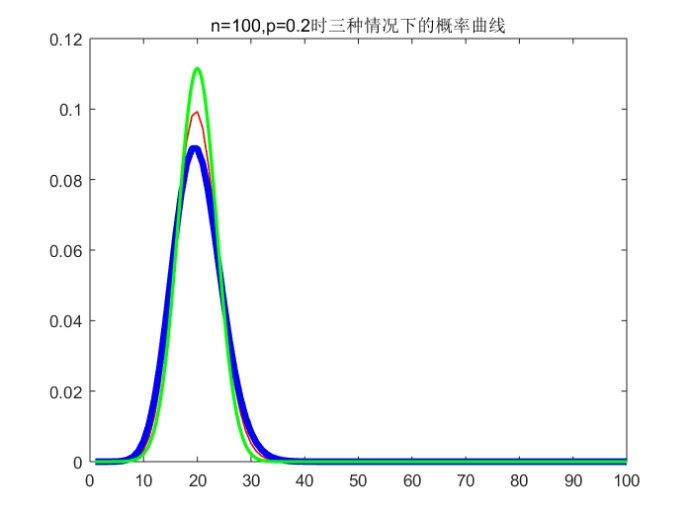
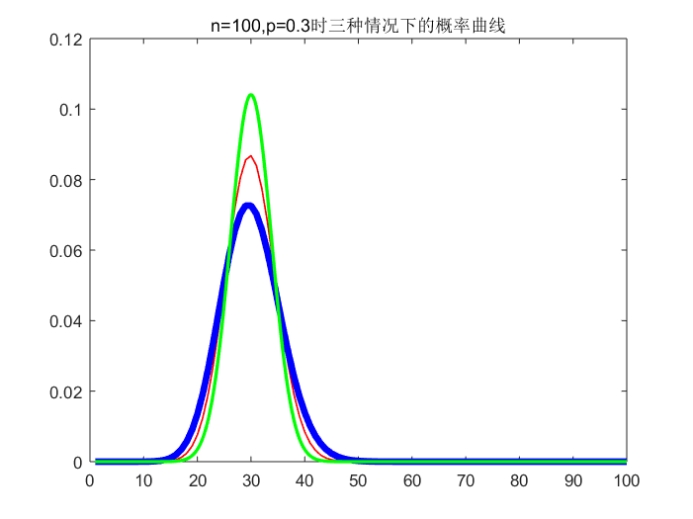
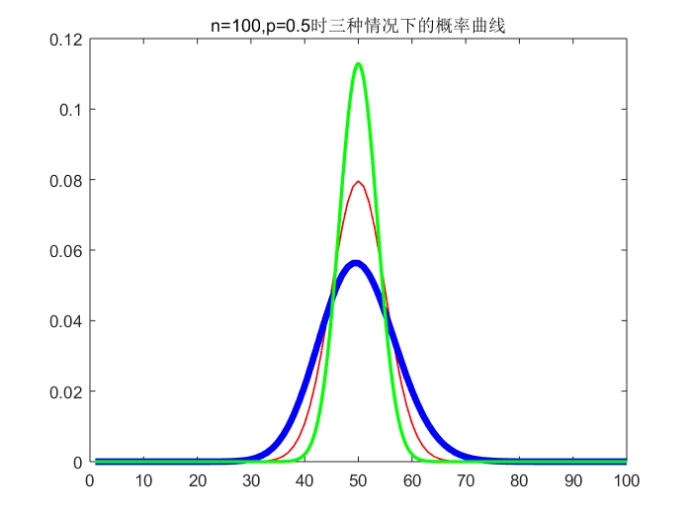
小结：从运行结果来看，在n较大时，p对于两种近似计算的精度影响都比较大，p越大，二者的近似精度都减小（图四），p比较小（约为0.1-0.2左右）时有比较好的近似效果（图一）。从中可以看出小概率二项分布在n比较大时用泊松分布和二项分布都可以较好地近似代替。当p增大而n不变时，对于两种近似计算都会产生较大的误差。

（b）

Ps：标准是红色（最细）、泊松是蓝色（最粗）、正态是绿色（中等粗细）

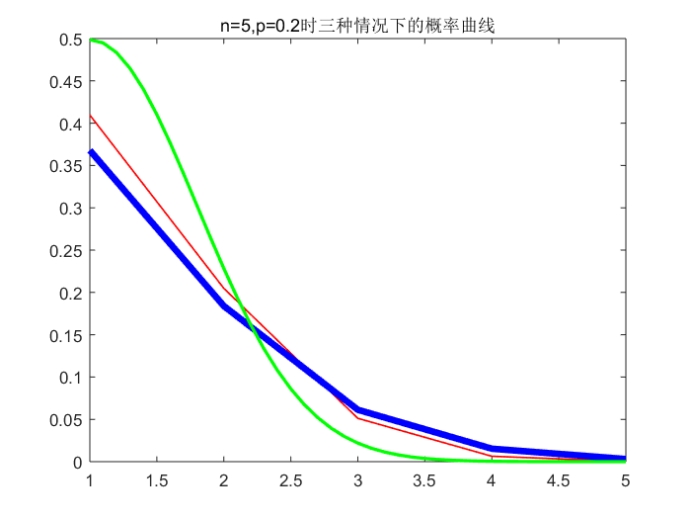
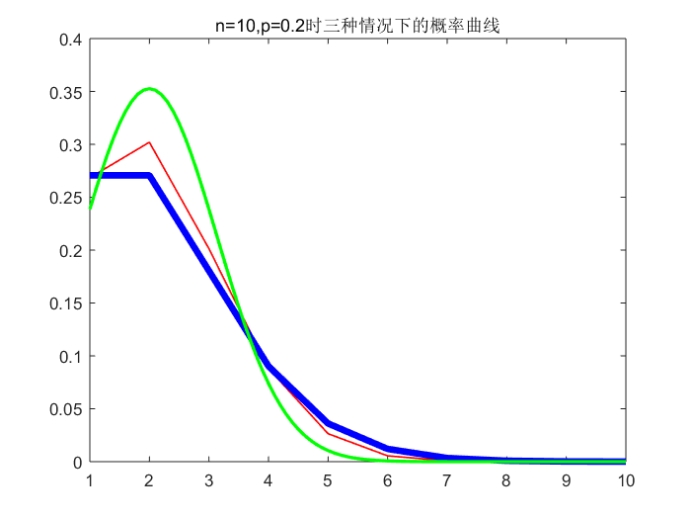
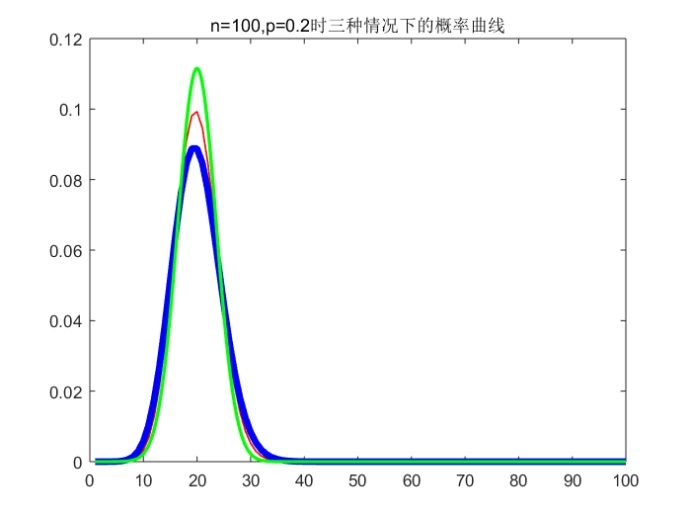
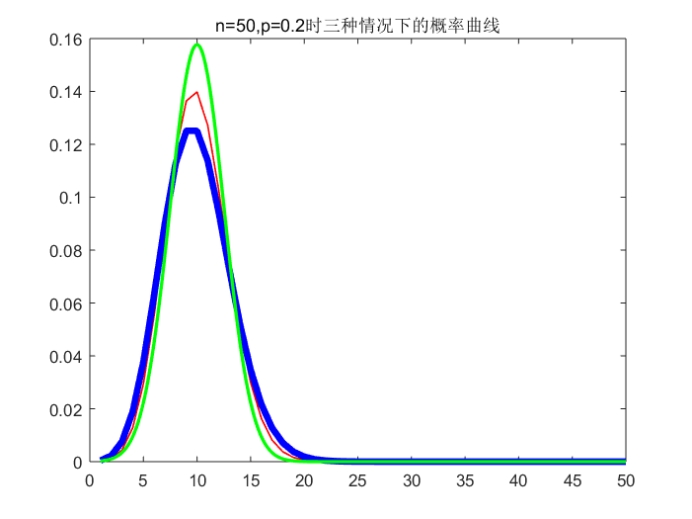
小结：从运行结果可以看出，当p取比较小的值（0.2）时，随着n的增长，两种近似分布对于精确分布的近似效果都变好了。在n比较小（np<5）时，正态分布对于二项分布的近似效果没有泊松分布好，只有当n充分大时，正态分布对于二项分布的近似效果才能更加精确。从中我们也能看出，在做近似时，n越大近似效果越好，在np<5时，用泊松分布近似二项分布比用正态分布近似效果好。

第二题

二、对正态总体参数的区间估计，进行验证及区间长度的变化情况（注：对一个参数，验证一种情形即可）。

（a）样本容量固定，置信度变化；（b）置信度固定，样本容量变化。

样本容量固定为8，α=0.05或0.1

源程序：α=0.05

1
2
3

x=[5.08,4.97,5.12,5.05,4.95,4.9,5.0,5.01];

[mu,sigma,muci,sigmaci]=normfit(x,0.05)

运行结果：

mu =

5.0100

sigma =

0.0717

muci =

4.9500

5.0700

sigmaci =

0.0474

0.1460

其置信度为95%的置信区间为（4.9500，5.0700）

源程序：α=0.1

1
2
3

x=[5.08,4.97,5.12,5.05,4.95,4.9,5.0,5.01];

[mu,sigma,muci,sigmaci]=normfit(x,0.1)

运行结果：

mu =

5.0100

sigma =

0.0717

muci =

4.9620

5.0580

sigmaci =

0.0506

0.1289

其置信度为90%的置信区间为（4.9620， 5.0580）

样本数为8时

置信度	置信区间	置信区间长度
α=0.1	（4.9620，5.0580）	0.0960
α=0.05	（4.9500，5.0700）	0.1200

b.样本数变为9，α=0.05

1
2
3

x=[5.08,4.97,5.12,5.05,4.95,4.9,5.0,5.01,5.01];

[mu,sigma,muci,sigmaci]=normfit(x,0.05)

mu =

5.0100

sigma =

0.0671

muci =

4.9584

5.0616

sigmaci =

0.0453

0.1285

置信度为95%的置信区间变短为（4.9584，5.0616）

置信度α=0.05时

样本数	置信区间	置信区间长度
8	（4.9500，5.0700）	0.1200
9	（4.9584，5.0616）	0.1032

小结：

选取了一组样本的观测值，本体假设参数服从正态总体N(5,0.7)，当样本容量固定，置信度越大，它的置信区间就越小，同样，当置信度固定，样本容量越大它的置信区间会越小。这也符合数理统计中的知识点，置信度和置信区间不能同时优化，而我们所获取的信息越多，我们就越能肯定置信区间。

第三题

三、自己选一个总体，验证样本k阶矩的观察值随样本容量的增大与总体k阶矩接近程度。

（对k=1,2进行验证）

源程序：

m = 1; % 分布的均值

v = 2; % 分布的方差

mu = log((m^2)/sqrt(v+m^2)); % 公式中的均值参数

sigma = sqrt(log(v/(m^2)+1)); % 公式中的方差参数

 

[M,V]= lognstat(mu,sigma); % 可以验证随机数的均值与方差的正确性

 

X = lognrnd(mu,sigma,1,1e6); % 产生随机数

n=length(X)

y=sum(X.^1)/n

hist(log(X), 100) % 画出随机数的对数正态分布函数图

运行结果：

（a）选择正态总体，k=1时，一阶矩为1

n =

10000

y =

0.9855

n =

100000

y =

0.9955

n =

1000000

y =

1.0007

n	10000	100000	1000000
y	0.9855	0.9955	1.0007
绝对差值	0.0145	0.0045	-0.0007

（b） K=2 正态总体的二阶矩为3

n =

10000

y =

3.0321

n =

100000

y =

2.9656

n =

1000000

y =

3.0244

n =

10000000

y =

3.0202

n =

100000000

y =

2.9986

n	10000	100000	1000000	10000000	100000000
y	3.0321	2.9656	3.0244	3.0202	2.9986
绝对差值	0.0321	0.0344	0.0244	0.0202	0.0014

小结：

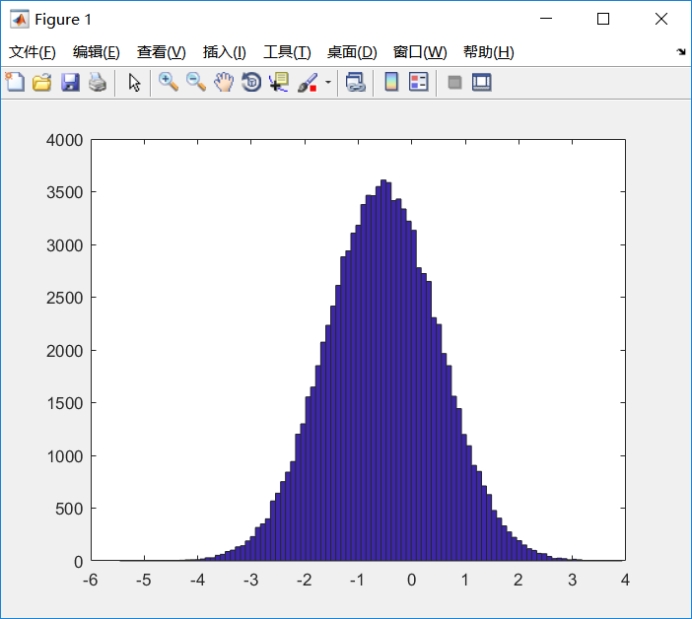
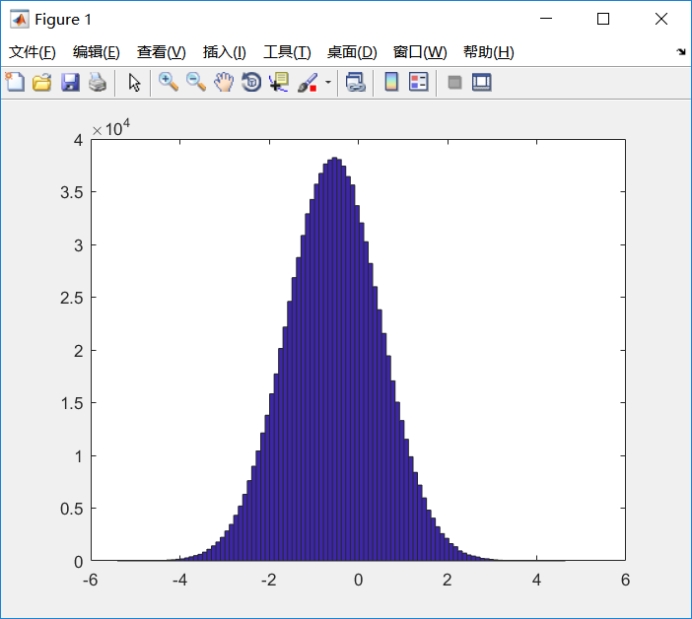
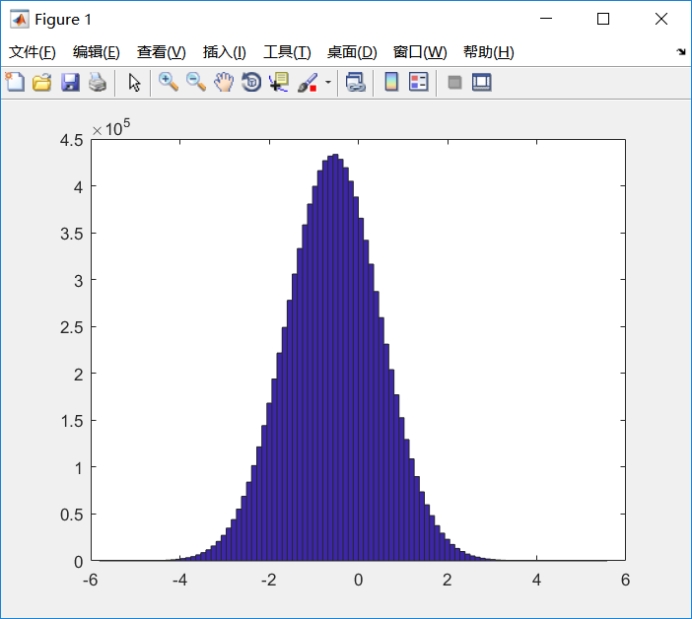
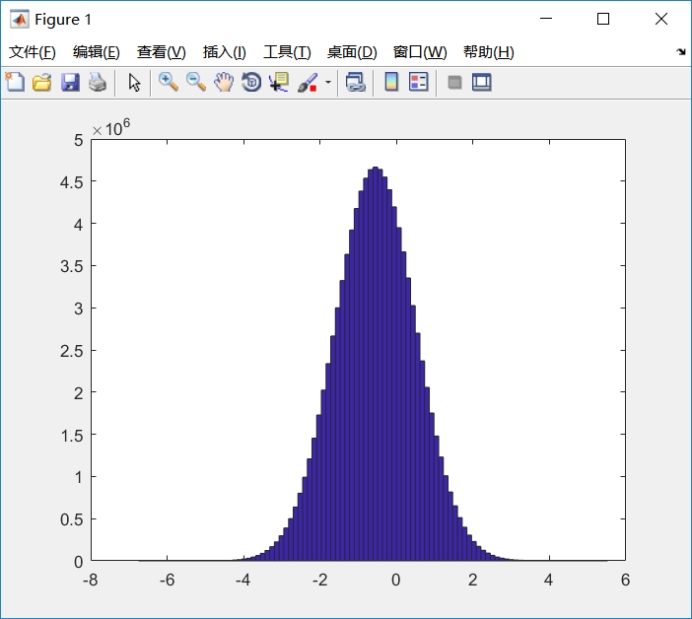
实验中选择了随机数产生正态分布而产生样本，随着样本数量增多，图像越来越符合正态分布，而且样本k阶矩的观察值随样本容量的增大与总体k阶矩接来越接近。

第四题

四、自己设计一种情形，当样本至少为多少时，产品的合格率才能符合给定的合格率。

合格率服从N（0.96，9），对其进行假设检验，n从0开始增加，在α<=0.05时记录n的值。循环1000次取均值。进行多次运行发现数值稳定在20~21附近。

源程序：

for i=1:1000

n=1;

sig=0;

while sig<0.95

  x=normrnd(0.96,3,1,n);

  [h,sig,ci]=ztest(x,0.96,3,0.05,0);

  n=n+1;

end

m(i)=n;

end

mean(m)

运行结果：

ans =

21.3680

ans =

21.4210

ans =

20.2820

ans =

20.0780

ans =

20.9050

ans =

21.5140

序号	1	2	3	4	5	6	均值
结果	21.3680	21.4210	20.2820	20.0780	20.9050	21.5140	20.9280

小结：本题假设合格率服从N（0.96，9），按此分布生成n个随机数，对其进行假设检验，n从0开始增加，在α<=0.05时记录n的值。循环1000次取均值。进行多次运行发现数值稳定在20~21附近。一共运行了六次，结果如上表，其平均值为20.9280。所以在假设前提下，样本至少为21时合格率才能在α<0.05的前提下达到要求。

第五题

五、产生卡方分布的随机数，并在一个坐标图中画出该卡方分布的统计直方图与真实卡方分布图形。

源程序：

n=100000;k=5;

for i=1:n

x(i)=chi2rnd(k);

end       %生成服从以k为自由度卡方分布的n个随机数向量x

hist(x,0:3:60)  %画x的频数分布直方图

hold on

y=0:0.1:60;

px=chi2pdf(y,k);

plot(y,px*3*n,'r-') %画以k为自由度的卡方分布概率密度曲线

title('n=5')

运行结果：

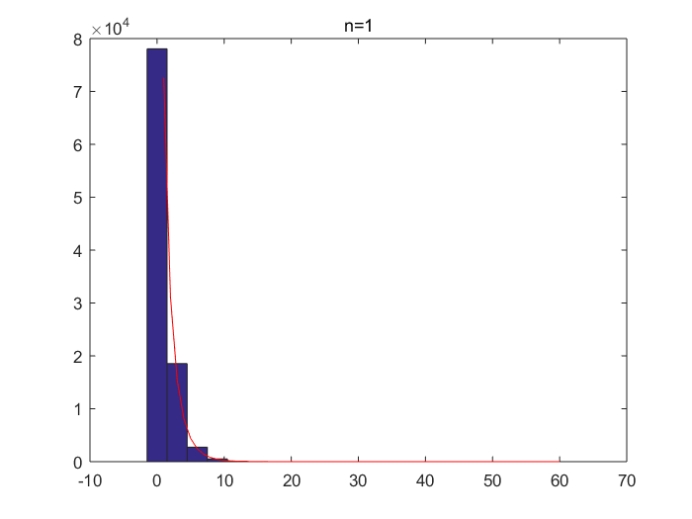
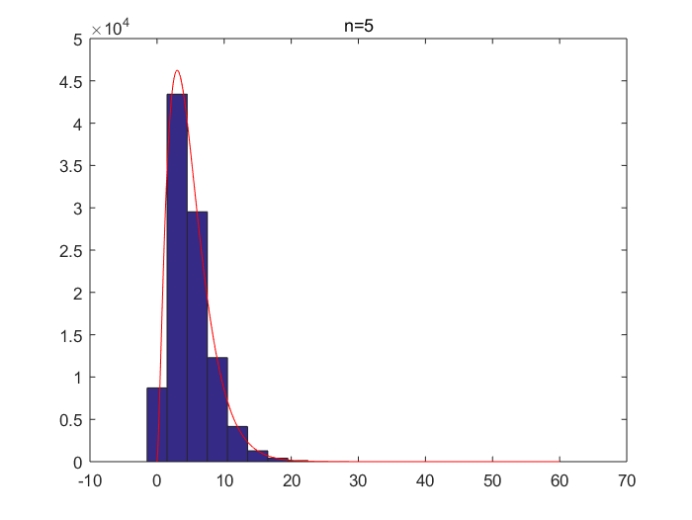
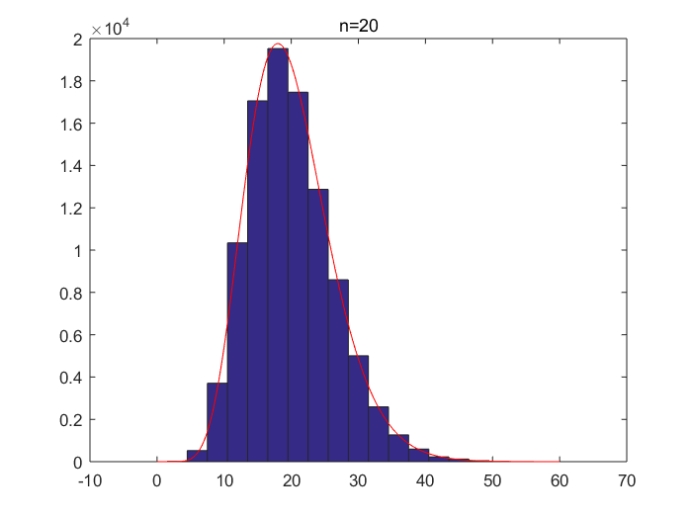
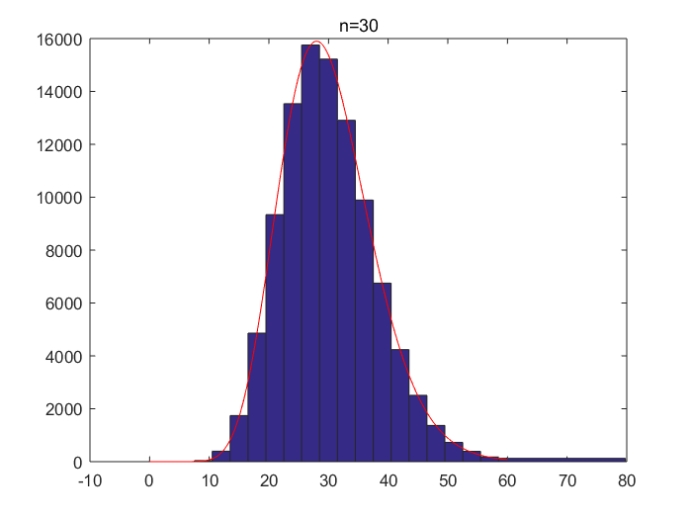
小结：

本题首先了确定了采样点数与卡方分布的“n”值（即程序中的k)，按照自由度为k的卡方分布、利用循环生成了n个随机数。接下来，画出频数直方图。然后，画出自由度为k的卡方分布的概率密度曲线。对k从1～30取了4个离散值，得出四个不同图样。分析可得，k值越小，样本的中心值越小；k值越大，样本的中心值越大。同时，k值越大，频数直方图与概率密度曲线的拟合度越高；k值越小，拟合度越低。

感想与体会：

本学期的概率统计与随机过程课程马上就要结束了，也是时候借着这样的一个机会来总结一下我一个学期学习的心得体会。

在刚开始接触概率论部分时，它给我的感觉就像是高中学的概率部分的内容，利用排列组合或者几何概型来计算概率。包括事件的独立性、随机事件等等看似朴实的概念，却是概率论这门课的基石。贝叶斯公式是我接触的第一个公式，在查阅资料后我发现，它在工程、经济等等各行各业都有着重要的用处。其实，概率统计在我们平时的学习中有许多的体现，在系统地学习了这门课以后，我对于事物的看法也有了变化。大一时大学物理实验中做数据处理，方差要除以（n-1）当时感觉很奇怪，因为这与高中学的除以n不同，查阅资料也没有得出什么结果。在学习了概率统计以后我知道了因为这些数据都是样本随机变量的观测值，而样本的方差做这样的定义是为了让它的期望刚好等于总体的方差，即总体的方差是它的无偏估计量。而在电路、模电实验当中示波器中波形有时会产生噪声，学了概率统计以后知道了看似没有规律的噪声信号也是符合某种规律的，只有掌握了其内在的分布规律才能想办法把它去除。

看似很好理解的概率统计概念其实是有理论支撑的，中学时只有一个模糊的概念，就是频率的极限是概率，但是却没有想一想这是为什么，只是认为它是真理罢了。在大数定律的学习中，我才发现，看似简简单单的道理，其背后都是有严格的证明的，人类现如今的成就，建立在这些看似简简单单的“真理”上，而这些理论背后是无数科学家的努力。在假设检验与参数估计章节，我接触了许许多多的工程与生活实际，利用概率统计的知识可以用了估计未知的随机变量的参数、估计其分布区间；也可以来检验某种说法是否正确，这也是把纯理论应用到了实际生活中。任何学科都有其应用的范围，而向概率统计这种基础学科更是应用在了方方面面。

随机过程是一门全新的学科，随机过程的理论产生于本世纪初期，是应物理学、生物学、管理科学等方面的需要而逐步发展起来的。目前，在自动控制、公用事业、管理科学等方面都有广泛的应用。由此看来，随机过程与我的专业关系密切。在刚接触这个学科的时候发现，虽然它应用了概率统计的知识，是在概率统计的基础上发展起来的，但它也有自己完整的一套理论。在实际应用中会用到极深的数学功底，动辄多重积分也是一个难点，不过在计算机发展至今的现在，许多复杂的计算不需要人来进行，所以说这在一定方面来说也促进了随机过程的发展。在学习时也应该作为重点而不是一带而过，正如老师所说的，许多在以后非常重要的知识，在刚开始学习的时候可能仅仅提了一下，而作为自动控制专业的学生，学好随机过程是非常重要的。

在之前接触到的许多文学、科普作品中，概率论给我的感觉，就像是宇宙最神秘的宝藏。因为在量子力学还没有发展的过去，决定论盛行，甚至还有“拉普拉斯妖”的假说。但是人们后来发现，完完全全精确地预言未来是做不到的。未来仅仅是一连串的概率，我们能做的，就是尽可能地增大自己希望发生的事情的概率。人类是渺小的，却也是强大的。渺小到无法完完全全掌握哪怕一个原子的精确参数，强大到能够用概率论去改变世界，去预测未来。

有一个微信公众号叫做“概率论”，其实是一个文艺号。但是仔细想想，我们的生活何尝不是由概率组成，茫茫人海中人和人的相遇也是一次观测下的小概率事件啊。