2020-05-28

利用BP网络实现非线性函数映射（基于matlab工具箱）

全文共: 3.2k字 | 阅读时长: 13分

阅读

文章导航

大三智能控制课程大作业，基于matlab的神经网络简单实现与训练

实验目的：自己设计一个BP网络实现非线性函数映射

基本要求：设有两输入单输出函数

其中自变量x,y的取值范围为试设计一个BP网络实现此函数映射。要求以完整的实验报告形式描述网络的结构、学习过程、结果，以附录形式附源程序。

一、网络结构

首先建立简单的BP神经网络模型，隐层神经元个数为10，输入二维，为函数的两个自变量x和y，输出为函数值的估计值，为一维。

在这里插入图片描述

在此基础上建立三层BP神经网络，两个隐层神经元个数都为10，输入二维，为函数的两个自变量x和y，输出为函数值的估计值，为一维。

二、学习过程

使用自己编写的子函数GetInput生成训练数据，可以自行指定生成的数据个数。调用格式为：[Input,Output] = GetInput(SampleNum)

（1）首先尝试自己通过编程实现简单的BP网络

参数设置为：总体样本30个，其中训练样本21个，验证样本5个，测试样本4个。最多训练次数为10000次，允许误差选为10-7，学习速率为0.01。传输函数为（purelin）最简单的一一对应关系。训练算法为梯度下降法，不断地对权值矩阵W1、W2，阈值矩阵B1、B2进行修正，最终达到训练效果。

（2）利用matlab自带的神经网络工具箱搭建BP网络

备注：也尝试了GUI界面编程，但是无法以代码形式展现，其工作过程与命令行操作相同。一共构建了两个网络：10-10-1和10-1，即第一部分中提到的两个网络。网络10-10-1参数设置为：总体样本分别为100个和1000个，其中训练样本70%，验证样本15%，测试样本15%。最多训练次数为10000次，允许误差选为，学习速率为0.01，动量因子为0.9。隐层传输函数为（tansig），输出层传输函数为（purelin）。训练算法为神经网络训练中常用的L-M算法（trainlm）网络10-1参数设置为：总体样本分别为100个、300个、500个和1000个，其中训练样本70%，验证样本15%，测试样本15%。最多训练次数为10000次，允许误差选为10-7，学习速率为0.01，动量因子为0.9。隐层传输函数为（tansig），输出层传输函数为（purelin）。训练算法为神经网络训练中常用的L-M算法（trainlm）

三、学习结果

（1）自己编程搭建的BP神经网络

30个训练样本和30个随机样本的验证结果

网络学习结果拟合图

（2）神经网络工具箱搭建的BP网络

Net1：10-10-1，100个样本

Net2：10-1，100个样本

Net3：10-1，300个样本

Net4：10-1，500个样本

Net5：10-1，1000个样本

Net6：10-10-1，1000个样本

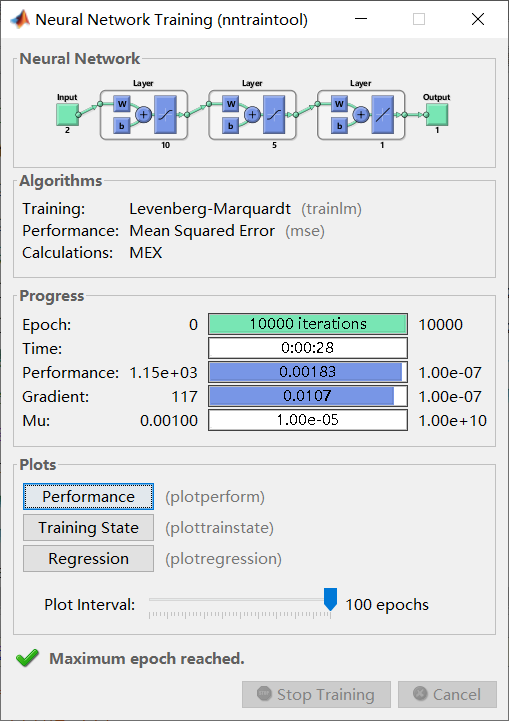
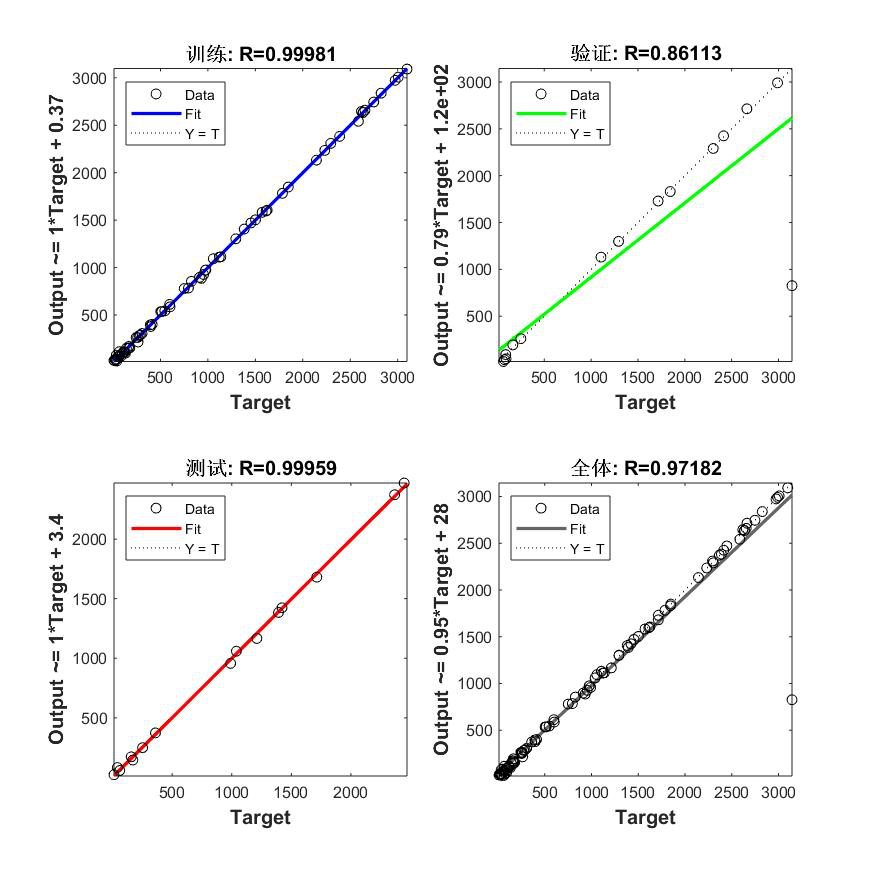
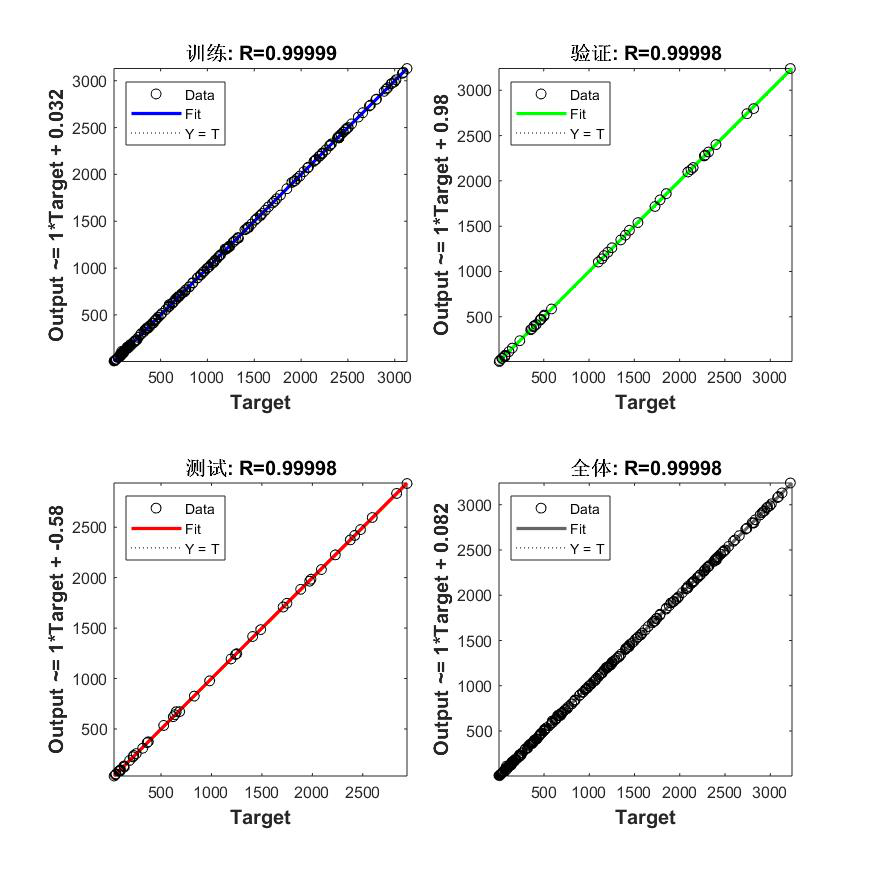
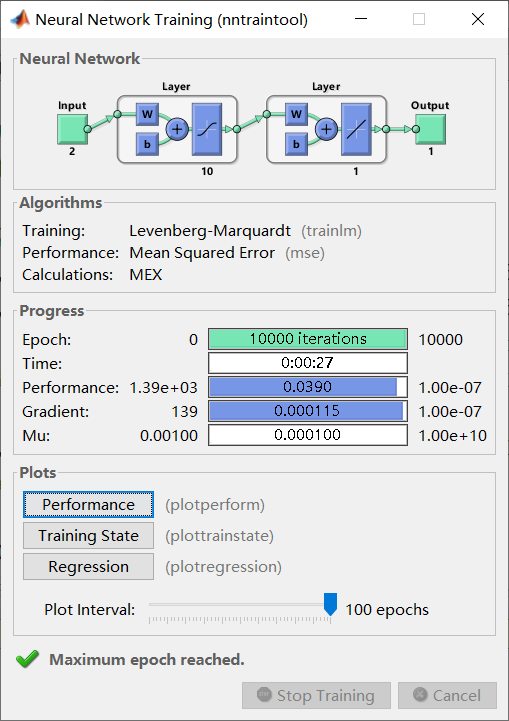
四、误差分析

（1）自己编程搭建的BP神经网络

标准差：3.5937

（2）神经网络工具箱搭建的BP网络

标准差：
40.4614 / 0.8592 / 0.0310 0.5113 / 0.2013 / 0.2013

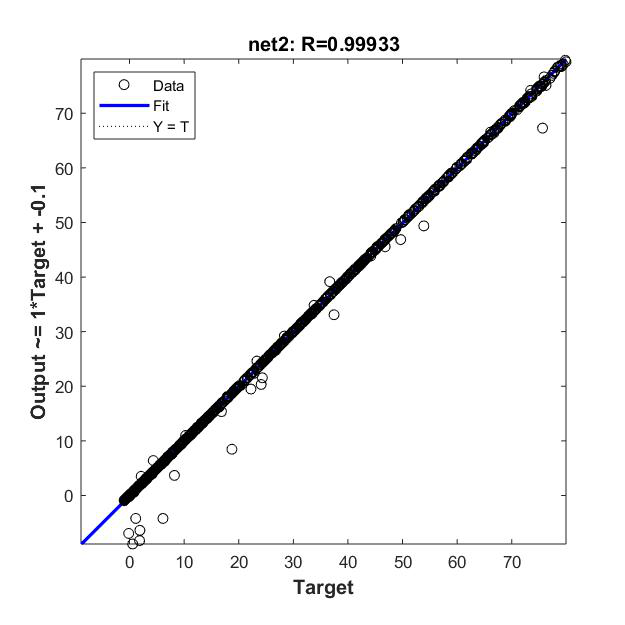
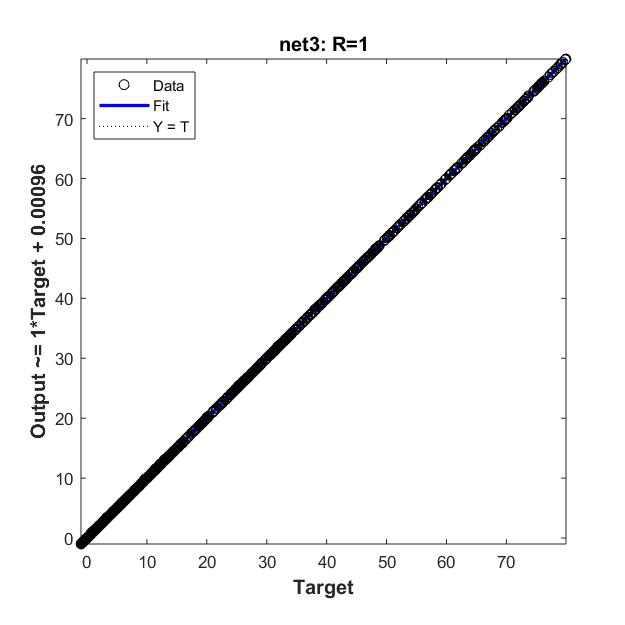
五、实验总结

这次实验中，我先尝试使用matlab自己编写了BP神经网络，输入映射函数使用最简单的y=x，训练算法采用梯度下降法。在实际操作中我发现当训练样本数大于28时，极有可能会陷入局部最优解，导致神经网络误差偏大，当训练样本数大于57时，误差甚至会随着迭代次数的增加而发散，这也是最基础的神经网络中难以避免的问题。20多个训练样本是比较合适的，所以总样本数选取了30。在训练样本和随机样本的检测下都显示出了比较好的效果。最后误差检验的结果显示，拟合图比较均匀地分布在直线两侧，标准差也不算太大。由于经典梯度下降法有着各种各样的问题，我在调用神经网络工具箱时采用了现在普遍使用的L-M算法，同时也尝试搭建了三层的BP神经网络。在两层神经网络中，预测精度得到了明显的提高，而且随着训练样本的增加，精度也有提高的趋势。然而事情也并非绝对，在精度达到一个阈值时，即使增加样本，精度也不会有明显的提高。而且训练有着一定的偶然性，即使样本数很少，初始条件选择合适的话也会比样本数多的模型精度更高。而三层网络在训练样本数少时预测效果反而没有两层的好，当样本数较多时效果和两层模型相同，这也提醒我，当问题比较简单时，不要贸然增加网络深度，有时候网络过深也不见得是一件好事。

附录（源程序）

（1）自编训练函数：

% function main()
clc                          % 清屏
clear all;                  %清除内存以便加快运算速度
close all;                  %关闭当前所有figure图像
Num=30;                   %所有样本总个数
TrainSamNum=0.7*Num;              %输入样本数量为21
ValSamNum=1/6*Num;               %验证样本数量为5
TestSamNum=2/15*Num;              %测试样本数量也是4
HiddenUnitNum=10;            %中间层隐节点数量取10
InDim=2;                    %网络输入维度为2
OutDim=1;                   %网络输出维度为1

%原始数据 
[p,t] = GetInput(Num);%生成输出p和输入t
%输入数据矩阵p
%目标数据矩阵t
[SamIn,minp,maxp,SamOut,mint,maxt]=premnmx(p,t); %原始样本对（输入和输出）初始化,进行了数据的归一化
[TrainSamIn,ValSamIn,TestSamIn] =divideblock(SamIn,0.7,1/6,2/15);
[TrainSamOut,ValSamOut,TestSamOut] =divideblock(SamOut,0.7,1/6,2/15);
rand('state',sum(100*clock))   %依据系统时钟种子产生随机数         
NoiseVar=0.01;                    %噪声强度为0.01（添加噪声的目的是为了防止网络过度拟合）
Noise=NoiseVar*randn(1,TrainSamNum);   %生成噪声
TrainSamOut=TrainSamOut + Noise;                   %将噪声添加到输出样本上

MaxEpochs=10000;                              %最多训练次数为10000
lr=0.01;                                      %学习速率为0.01
E0=1e-7;                                      %目标误差为1e-7
W1=0.5*rand(HiddenUnitNum,InDim)-0.1;   %初始化输入层与隐含层之间的权值
B1=0.5*rand(HiddenUnitNum,1)-0.1;       %初始化输入层与隐含层之间的阈值
W2=0.5*rand(OutDim,HiddenUnitNum)-0.1; %初始化输出层与隐含层之间的权值              
B2=0.5*rand(OutDim,1)-0.1;                %初始化输出层与隐含层之间的阈值
W11=W1;W22=W2;B11=B1;B22=B2;

ErrHistory=[];                              %给中间变量预先占据内存
for i=1:MaxEpochs
    
    HiddenOut=logsig(W1*TrainSamIn+repmat(B1,1,TrainSamNum)); % 隐含层网络输出
    NetworkOut=W2*HiddenOut+repmat(B2,1,TrainSamNum);    % 输出层网络输出
    Error=TrainSamOut-NetworkOut;                       % 实际输出与网络输出之差
    SSE=sumsqr(Error);                               %能量函数（误差平方和）

    ErrHistory=[ErrHistory SSE];

    if SSE<E0,break, end      %如果达到误差要求则跳出学习循环
    
    % 下面是权值（阈值）依据能量函数负梯度下降原理所作的每一步动态调整量
    Delta2=Error;
    Delta1=W2'*Delta2.*HiddenOut.*(1-HiddenOut);    

    dW2=Delta2*HiddenOut';
    dB2=Delta2*ones(TrainSamNum,1);
    
    dW1=Delta1*TrainSamIn';
    dB1=Delta1*ones(TrainSamNum,1);
    %对输出层与隐含层之间的权值和阈值进行修正
    W2=W2+lr*dW2;
    B2=B2+lr*dB2;
    %对输入层与隐含层之间的权值和阈值进行修正
    W1=W1+lr*dW1;
    B1=B1+lr*dB1;
end
SSE   %显示最终误差

%拟合图
TrainHiddenOut=logsig(W1*TrainSamIn+repmat(B1,1,TrainSamNum)); % 隐含层输出最终结果
TrainNetworkOut=W2*TrainHiddenOut+repmat(B2,1,TrainSamNum);    % 输出层输出最终结果
Trainoutput=postmnmx(TrainNetworkOut,mint,maxt);               % 还原网络输出层的结果
ValHiddenOut=logsig(W1*ValSamIn+repmat(B1,1,ValSamNum)); % 隐含层输出最终结果
ValNetworkOut=W2*ValHiddenOut+repmat(B2,1,ValSamNum);    % 输出层输出最终结果
Valoutput=postmnmx(ValNetworkOut,mint,maxt);               % 还原网络输出层的结果
TestHiddenOut=logsig(W1*TestSamIn+repmat(B1,1,TestSamNum)); % 隐含层输出最终结果
TestNetworkOut=W2*TestHiddenOut+repmat(B2,1,TestSamNum);    % 输出层输出最终结果
Testoutput=postmnmx(TestNetworkOut,mint,maxt);               % 还原网络输出层的结果
[TrainSamOut,ValSamOut,TestSamOut] =divideblock(t,0.7,1/6,2/15); %还原原始输出
Tolvalue=[TrainSamOut,ValSamOut,TestSamOut];
Toloutput=[Trainoutput Valoutput Testoutput];
figure
plotregression(TrainSamOut,Trainoutput,'训练',ValSamOut,Valoutput,'验证',...
    TestSamOut,Testoutput,'测试',Tolvalue,Toloutput,'全体')

%绘制网络输出与真实输出的对比图
HiddenOut=logsig(W1*SamIn+repmat(B1,1,Num)); % 隐含层输出最终结果
NetworkOut=W2*HiddenOut+repmat(B2,1,Num);    % 输出层输出最终结果
newk=postmnmx(NetworkOut,mint,maxt);               
x=1:Num; 
figure
subplot(2,1,1);plot(x,newk,'r-o',x,t,'b--+')    %绘对比图；
legend('网络输出','实际输出');
title('训练样本的预测结果')
[p1,t1] = GetInput(Num);%生成检验的输出p1和输入t1
[SamIn1,minp,maxp]=premnmx(p1);%归一化
HiddenOut=logsig(W1*SamIn1+repmat(B1,1,Num)); % 隐含层输出最终结果
NetworkOut=W2*HiddenOut+repmat(B2,1,Num);    % 输出层输出最终结果
newk1=postmnmx(NetworkOut,mint,maxt);
subplot(2,1,2);plot(x,newk1,'r-o',x,t1,'b--+')    %绘对比图；
legend('网络输出','实际输出');
title('随机验证的预测结果')

误差检验：

[p,t] = GetInput(1000);%生成输出p和输入t
[SamIn,minp,maxp,tn,mint,maxt]=premnmx(p,t); %原始样本对（输入和输出）初始化,进行了数据的归一化
HiddenOut=logsig(W1*SamIn+repmat(B1,1,1000)); % 隐含层输出最终结果
NetworkOut=W2*HiddenOut+repmat(B2,1,1000);    % 输出层输出最终结果
newk=postmnmx(NetworkOut,mint,maxt);               
figure;plotregression(t,newk,'自编函数')
E = t-newk;
std(E)
% 一次运行结果：3.5937

（2）神经网络工具箱训练函数：

clear all
[p,t] = GetInput(30);%生成输出p和输入t
[p1,ps]=mapminmax(p);%归一化
[t1,ts]=mapminmax(t);
%分割为训练数据、验证数据、测试数据
[trainsample.p,valsample.p,testsample.p] =divideblock(p,0.7,0.15,0.15);
[trainsample.t,valsample.t,testsample.t] =divideblock(t,0.7,0.15,0.15);
%关于net函数的参数说明：net = newff(minmax(p),[隐层的神经元的个数，输出层的神经元的个数],...
% {隐层神经元的传输函数，输出层的传输函数｝,'反向传播的训练函数'),其中p为输入数据，t为输出数据
TF1='tansig';TF2='purelin';
net=newff(minmax(p),[10,1],{TF1 TF2},'trainlm');%创建BP神经网络，隐层10个神经元，两层（不包括输入层）
%训练算法为Levenberg-Marquardt算法
%网络参数的设置
net.trainParam.epochs=10000;%训练次数
net.trainParam.goal=1e-7;%训练精度
net.trainParam.lr=0.01;%学习率
net.trainParam.mc=0.9;%动量因子
net.trainParam.show=25;%显示间隔次数
[net,tr]=train(net,trainsample.p,trainsample.t);%训练网络
%计算仿真
[normtrainoutput,trainPerf]=sim(net,trainsample.p,[],[],trainsample.t);%训练的数据经BP得到的结果
[normvalidateoutput,validatePerf]=sim(net,valsample.p,[],[],valsample.t);%验证的数据经BP得到的结果
[normtestoutput,testPerf]=sim(net,testsample.p,[],[],testsample.t);%测试数据经BP得到的结果
%反归一化
trainoutput=mapminmax('reverse',normtrainoutput,ts);
validateoutput=mapminmax('reverse',normvalidateoutput,ts);
testoutput=mapminmax('reverse',normtestoutput,ts);
%真实数据
trainvalue=mapminmax('reverse',trainsample.t,ts);%正常的训练数据
validatevalue=mapminmax('reverse',valsample.t,ts);%正常的验证的数据
testvalue=mapminmax('reverse',testsample.t,ts);%正常的测试数据

%plotregression拟合图
tolvalue=[trainvalue validatevalue testvalue];
toloutput=[trainoutput validateoutput testoutput];
figure
plotregression(trainvalue,trainoutput,'训练',validatevalue,validateoutput,'验证',...
testvalue,testoutput,'测试',tolvalue,toloutput,'全体')

误差检验：

clear
load net.mat
e=zeros(1000,6);
Z=zeros(1000,1);
Y1=zeros(1000,1);
Y2=zeros(1000,1);
Y3=zeros(1000,1);
Y4=zeros(1000,1);
Y5=zeros(1000,1);
Y6=zeros(1000,1);
for i=1:1000
    a=rand(1)*4*pi-2*pi;
    b=rand(1)*4*pi-2*pi;
    y1 = sim(net1,[a;b]);%100样本三层10 5 1
    y2 = sim(net2,[a;b]);%100样本两层10 1
    y3 = sim(net3,[a;b]);%300样本两层10 1
    y4 = sim(net4,[a;b]);%500样本两层10 1
    y5 = sim(net5,[a;b]);%1000样本两层10 1
    y6 = sim(net5,[a;b]);%1000样本三层10 5 1
    z=2*a^2+sin(b+pi/4);
    Z(i)=z;Y1(i)=y1;Y2(i)=y2;Y3(i)=y3;Y4(i)=y4;Y5(i)=y5;Y6(i)=y6;
    e(i,:)=[z-y1 z-y2 z-y3 z-y4 z-y5 z-y6];
end
[std(e(:,1)) std(e(:,2)) std(e(:,3)) std(e(:,4)) std(e(:,5)) std(e(:,6))]
figure;plotregression(Z,Y1,'net1');
figure;plotregression(Z,Y2,'net2');
figure;plotregression(Z,Y3,'net3');
figure;plotregression(Z,Y4,'net4');
figure;plotregression(Z,Y5,'net5');
figure;plotregression(Z,Y6,'net6');
%一次运行结果 43.5757    0.6526    0.0305    0.4823    0.2029    0.2029

（3）生成训练样本的子函数

function [Input,Output] = GetInput(SampleNum)
Input=zeros(2,SampleNum);
Output=zeros(1,SampleNum);
for i=1:SampleNum
    x=rand(1)*4*pi-2*pi;
    y=rand(1)*4*pi-2*pi;
    z=2*x^2+sin(y+pi/4);
    Input(:,i)=[x,y];
    Output(i)=z;
end

（4）训练得到的网络

%见net.mat

本文之前发表在CSDN上，链接如下：原文地址