大数据作业1——apriori算法

全文共: 5.1k字   |   阅读时长: 20分
知识整理本科课程大四
  阅读

文章导航

大四上大数据分析与知识发现大作业——apriori算法

本报告主要工作：本次大作业使用python自己编程实现了apriori算法，并分别从分布式实现和事务压缩处理的角度进行了算法优化。从中医药网站爬取了两万多条药方作为数据集，用来挖掘各种中药材之间的关联规则，分别使用不同的支持度、置信度进行实验，取得了比较有趣的结果。同时也使用老师给的百货商店数据集进行了测试。

代码运行环境为Python 3.7.4，IDE为Pycharm，所有代码均为自己编写。参考书籍：《数据挖掘概念与技术》（原书第二版）、《机器学习实战》。

一、 关于关联规则的简要介绍

要介绍关联规则，首先要引入两个概念：事务和频繁项集。

事务：数据集中的一条内容，可以是一次消费的购买记录，也可以是一次测量的返回结果，或者是一个药方中的药品。可以理解为与某个事情相关的名词的集合。

频繁项集：要想介绍频繁项集，首先要介绍“项集”。顾名思义，“项集”就是项的集合，项就是每一条事务中的一个名词，可以代表一个物品或者一个事件。“频繁项集”就是在数据集中频繁出现的项集，即一种频繁的模式，这个项集可大可小，依据其在数据集中出现的频率而判断是否为频繁项集。

而关联规则是基于这二者进行计算的，它的基本定义为：

关联规则：两个项集之间所具有的某种相关关系，其紧密程度由支持度和置信度来衡量。我们将关联规则中前面的项集叫做前件，后面的项集叫做后件，规则的含义可以表示为：前件出现，后件将有很大概率出现。

下面介绍衡量关联规则的两条准则：支持度与置信度。

支持度：一个项集的支持度被定义为数据集中包含该项集的记录所占的比例

置信度：两个项集之间关联规则紧密程度的置信度可以理解为前后件的并集所代表的项集的支持度与前件支持度的比，即：出现前件的条件下出现后件的概率。

二、Apriori算法主要流程

为了寻找频繁项集，就必须计算每个项集的支持度，当事务中项的数目很多时，它们之间互相的排列组合就变得及其复杂。当数据集庞大时，每个事项的检测都包含的大量的比对和筛选，算法复杂度变得很高，计算时间成本极大。

为了解决这个问题，我们提出了apriori原理：如果某个项集是频繁项集，那么它所有的子集也是频繁的。即如果 {0,1} 是频繁的，那么 {0}, {1} 也一定是频繁的。这个规则看似直观，但需要经过极为严格的证明，所幸前人已经为我们证明好了这个定理。乍一看它似乎没什么用，但是把这个定理反过来，它的逆否命题为：如果某个项集非频繁，那么它的超集也非频繁。那么我们就可以在由小项集组合大项集时提前筛掉那些不频繁的项集，从而大大减少计算量。

算法的主要步骤为：

  1. 寻找频繁项集

①　扫描整个数据集获取所有单个名词的项集列表——候选1-项集。

②　扫描数据集计算每个候选1-项集的支持度，删除不满足最小支持度的项集，形成频繁1-项集，此时k=2。

③　对此时的频繁（k-1）-项集进行组合，形成候选的k-项集。若k-项集为空，退出。

④　扫描数据集计算每个候选k-项集的支持度，筛选出符合条件的k-项集，形成频繁k-项集。返回第三步。

  1. 寻找关联规则

使用递归的方法，遍历所有大于1的频繁项集，求取它们的1项集子集：

—如果是频繁2项集：

——使用差集的方法计算置信度，符合的关联规则直接输出。

—或者项集中项数大于等于3：

——如果子集可以继续组合成能生成其他规则的新子集：（1）

———子集进行组合，测试新生成的规则是否满足条件，符合的直接输出。

———如果还可以继续组合，递归调用（1）

​ 否则：

———继续遍历下一个项集

一些优化方法：

  1. 使用分布式的方法，将数据集分为多个块，在遍历数据集时利用python中的map函数，将比较统计的部分分开进行，再使用reduce函数整合每个块统计的结果，形成最终的答案。这对大规模数据集比较适用。

  2. 使用事务压缩的方法，在遍历数据集时，如果某个事务已经不包含当前的频繁k-项集，那么它们必然不包含由这频繁k-项集组成的候选k+1-项集，那么在下一次遍历时就可以跳过这些事务，不必再进行子集计算，节省了运行时间。这对大部分情况都比较适用。

三、 所采用的数据集简介

中医药的理论博大精深，各种药材之间的配合在治病的疗效上会起到1+1>2的效果。比如茯苓和人参搭配，具有益心力，除谬忘，能饮食，延年益寿之功效。主治上气，胸胁满闷，霍乱，积痢。其他的相似组合还有很多，进行关联规则的发现可以帮助我们更系统地归纳古人留下的药方中的知识，便于将中医药应用于现代疾病的治疗中。

所用我从某中医网站爬取了2万多条药方的数据，作为待挖掘的数据集，意在找出哪些药材之间的关联规则比较大，哪些药材常常出现并且被搭配使用在药方当中。爬取数据集的代码放在crawler.py文件中，2万条药方的网址已经提前爬出可以直接导入进行读取，节省时间。（url.csv）

中医网站页面（网址：http://zhongyaofangji.com/all.html）

药方详细页面

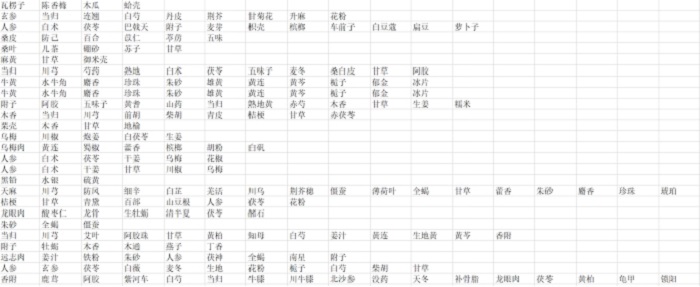
数据集展示（prescription.csv）

四、 实验结果分析

（1） 三种方式运行时间比较

选取prescription.csv药方数据（2万余条），最小支持度和最小置信度都为0.01

不同改进算法的运行时间比较表

运行时间 第一次 第二次 第三次 第四次 第五次 平均值
基本算法 36.0405 35.8101 34.1877 35.9658 33.7644 35.1537
分布式 34.2813 33.9013 34.2965 34.5172 34.3388 34.26702
事务压缩 31.0910 32.0156 31.2278 31.0221 31.6232 31.39594

从运行时间可以大致看出，分布式算法由于使用mapreduce并行执行，运行时间略有减少，但是并行运行会占用更多的内存，分布式的主要用处是在数据集过大无法全部导入内存时可以进行计算，在节省时间方面不是主流。而基于事务压缩的方法可以避免多次无用的遍历，所以在时间节约上也比较明显。

（2）修改支持度、置信度的结果

不同支持度、置信度比较表

置信度 支持度 0.01 0.05 0.1 0.2 0.3 0.4
0.01 频繁项集 419 419 419 419 419 419
关联规则 679 648 515 288 156 88
运行时间 30.6290 33.8207 32.0566 30.7340 31.0242 30.5041
.015 频繁项集 207 207 207 207 207 207
关联规则 255 255 219 139 82 51
运行时间 19.0702 20.9975 18.1798 18.6537 18.4798 18.5693
0.02 频繁项集 126 126 126 126 126 126
关联规则 119 119 113 79 48 31
运行时间 14.9484 14.8706 14.7600 14.6400 14.8406 14.9926
0.03 频繁项集 59 59 59 59 59 59
关联规则 36 36 36 29 21 15
运行时间 11.9174 11.9613 12.1243 12.0313 12.0253 11.8591
0.04 频繁项集 38 38 38 38 38 38
关联规则 22 22 22 18 13 10
运行时间 11.3005 11.3198 11.2225 11.3224 11.0737 11.3320
0.05 频繁项集 23 23 23 23 23 23
关联规则 10 10 10 10 7 6
运行时间 10.7939 11.0177 10.8461 10.9094 10.7684 10.7101
0.06 频繁项集 15 15 15 15 15 15
关联规则 4 4 4 4 2 2
运行时间 10.7497 10.5669 10.6482 10.7804 10.6141 10.6488

从上表可以看出： 支持度相同，最小置信度越高，关联规则数越少； 置信度相同，最小支持度越高，频繁项集数越少； 运行时间和最小支持度关系最大，最小支持度越大，运行时间越短； 关联规则的挖掘几乎不会影响到运行时间，因为比较的频繁项集数量级都很小； 随着最小支持度的增大，最小置信度的变化对发现的关联规则数量的影响减小； 最小置信度变化幅度不大时对发现的关联规则数目影响不大； 频繁项集和支持度的相关关系是非线性的，在某一区间内变化很明显。

（3）挖掘出的有趣规则

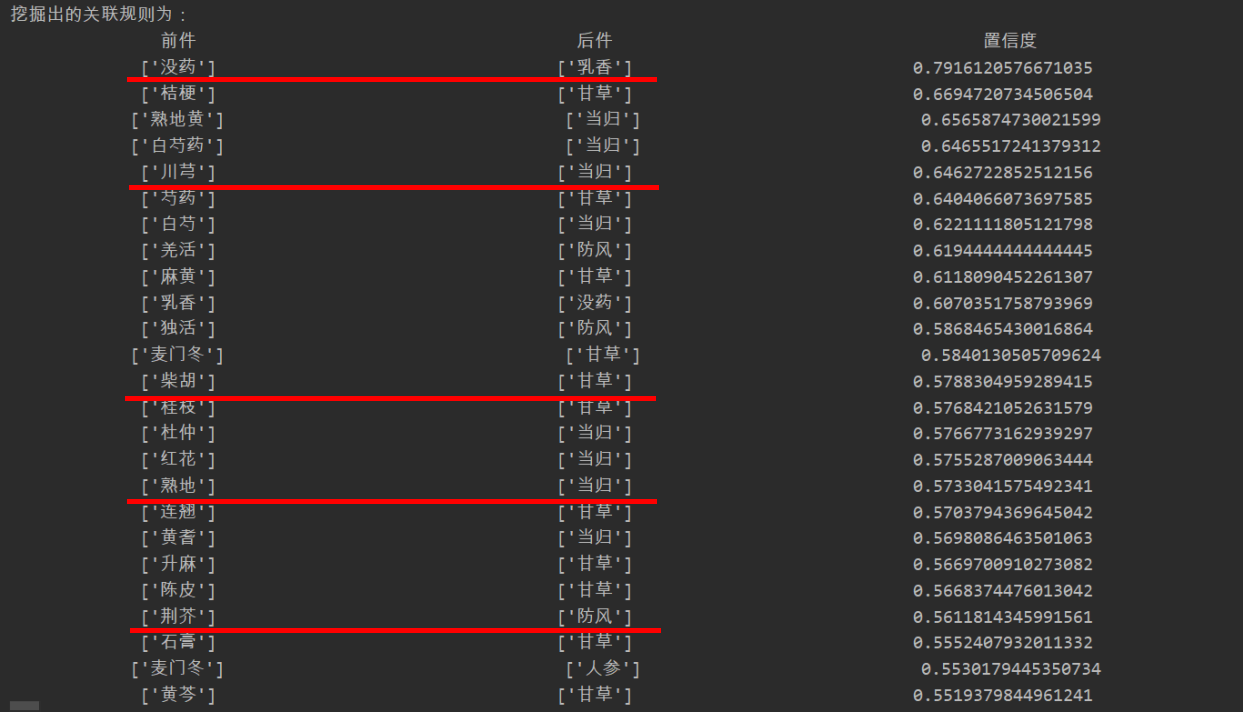
支持度、置信度均为0.01时前25项挖掘出的关联规则

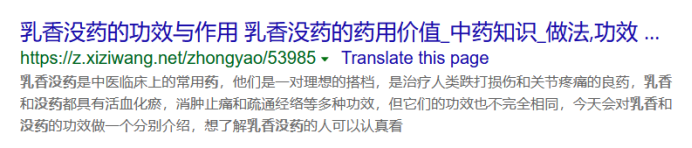
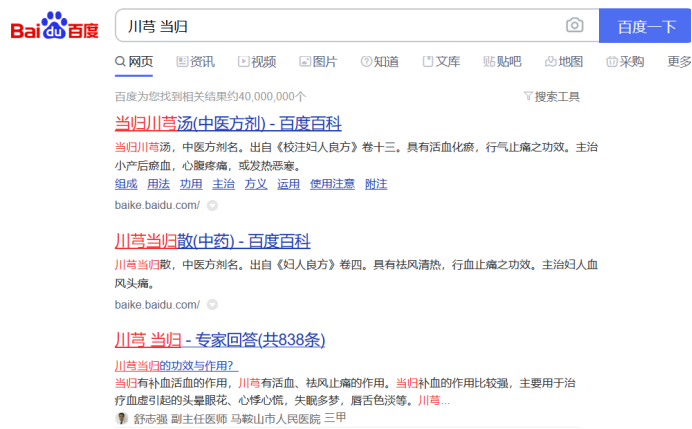
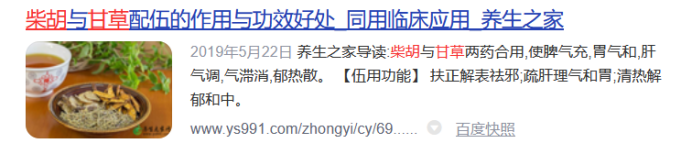
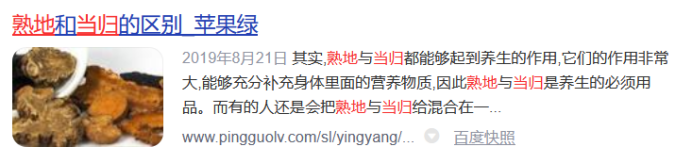
我们随机取其中的五条：没药->乳香；川芎->当归；柴胡->甘草；熟地->当归；

荆芥->防风。在搜索引擎中分别搜索这几种组合。

可以看出挖掘出的关联规则中的药物都有着很深的关系，至少人们经常把它们放在一起作为药方。

测试该条件下置信度最弱的一条关联规则：甘草->桂枝

即使是预设条件下关联规则最弱的一条也可以在网上找到相应的搭配，可见我们挖掘出的关联规则在统计意义下是有效的。

我们也注意到，在挖掘出的关联规则中，经常出现的中药材有甘草、人参、当归、白术、白芍、川芎等等，我们搜索中药方中最常用的药材：

相关的内容也几乎匹配。

（4）使用老师提供的百货商店数据集挖掘出的一些规则

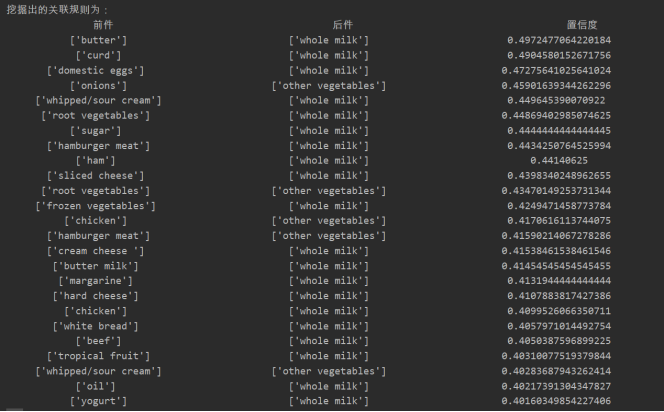
支持度、置信度均为0.01时前25项挖掘出的关联规则

对上述关联规则进行一定的分析可以发现一个比较有趣的事情：美国人在购物时比较偏爱“whole milk”，即全脂牛奶，在购买黄油、凝乳、鸡蛋、糖、汉堡肉、蔬菜等等食物之后都偏爱购买牛奶，这与他们的生活习惯不无关系。搜索相关内容也会发现类似的报道。

附录（源代码）

1. 基本Apriori算法代码：（basic.py）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
from numpy import *
from csv import reader
import time


# 导入数据集
def load_dataset(fileName):
    with open(fileName, 'rt', encoding='UTF-8') as raw_data:
        readers = reader(raw_data, delimiter=',')
        dataset = list(map(frozenset, readers))
    return dataset

# 以下为挖掘频繁项集相关函数


# 统计所有1-项集
def get_one_itemset(dataset):
    itemset = []    # 1-项集
    for affair in dataset:  # 遍历一遍数据集统计项集个数
        for item in affair:
            if [item] not in itemset:
                itemset.append([item])
    return list(map(frozenset, itemset))


# 通过候选k-项集的筛选，确定频繁k-项集
# 输入：数据集，候选k-项集，最小支持度； 输出：频繁k-项集列表，支持度字典
def get_freqset(dataset, itemset, minSupport):
    supportData = {}     # 支持度字典
    count = {}           # 计数字典
    freqset = []         # 频繁k-项集
    for affair in dataset:  # 遍历数据集计算候选项集频次
        for item in itemset:
            if item.issubset(affair):  # 如果候选项集是事务的子集，计数+1
                if item in count:
                    count[item] += 1
                else:
                    count[item] = 1
    number = len(dataset)  # 事务的数目
    for key in count:      # 遍历计数字典筛选符合条件的项集作为频繁项集，计算支持度
        support = count[key]/number
        if support >= minSupport:
            freqset.append(key)
            supportData[key] = support
    return freqset, supportData


# 由频繁k-项集求候选k+1-项集
# 输入：频繁k-项集，项集中的项数k； 输出：候选k+1-项集
def get_itemset(freqset, k):
    itemset = []       # 候选k+1-项集
    freqlen = len(freqset)  # 频繁项集个数（用于遍历）
    for i in range(freqlen):  # 遍历候选项集组合新项集
        for j in range(i+1, freqlen):
            item = freqset[i] | freqset[j]
            if len(item) == k and item not in itemset:  # 项数为k且之前未出现
                itemset.append(item)
    return itemset


# 挖掘所有满足条件的频繁项集
# 输入：数据集，最小支持度； 输出：频繁项集列表、支持度字典
def get_all_freqset(dataset, minSupport=0.001):  # 最小支持度默认0.001
    C1 = get_one_itemset(dataset)
    L1, supportData = get_freqset(dataset, C1, minSupport)
    print('已经挖掘频繁', 1, '项集...')
    freqset = [L1]
    k = 0
    while len(freqset[k]) > 0:  # 循环，直到挖掘完毕所有的频繁项集（最后一项为空）
        Ck = get_itemset(freqset[k], k+2)  # 求候选项集
        Lk, support = get_freqset(dataset, Ck, minSupport)  # 求频繁项集和支持度字典
        freqset.append(Lk)
        supportData.update(support)
        k += 1
        print('已经挖掘频繁', k+1, '项集...')
    return freqset, supportData

# 以下函数为挖掘关联规则相关函数


# 测试筛选符合最小置信度的关联规则
# 输入：频繁项集、频繁项的子集列表、支持度字典、规则集合、最小置信度； 输出：符合最小置信度条件的频繁项子集列表
def test_rule(freqset, subset, supportData, rules, minConfi):
    trueSubset = []
    for item in subset:  # 测试每一个子集与对应项集生成的规则是否满足条件
        confi = supportData[freqset]/supportData[freqset-item]
        if confi >= minConfi:  # 满足条件即加入规则库
            rules.append((freqset-item, item, confi))
            trueSubset.append(item)
    return trueSubset


# 递归地遍历各种可能的规则组合，从单元素子集开始构建多元素子集来划分项集生成规则，不满足最小置信度的频繁项子集不参与新子集的构建
# 输入：频繁项集、频繁项的子集列表、支持度字典、规则集合、最小置信度
def form_subset(freqset, subset, supportData, rules, minConfi):
    itemNum = len(subset[0])  # 求子集元素个数，用于判断是否迭代
    if len(freqset) > (itemNum+1):  # 子集可以组合形成可以生成完整规则的新子集
        newSubset = get_itemset(subset, itemNum+1)  # 子集进行组合
        newSubset = test_rule(freqset, newSubset, supportData, rules, minConfi)
        if len(newSubset) > 1:  # 还可以继续组合
            form_subset(freqset, newSubset, supportData, rules, minConfi)


# 求关联规则
# 输入：频繁项集、频繁项集支持度字典、最小置信度（默认0.01）； 输出：关联规则元组列表
# 关联规则元组结构：前件、后件、置信度
def get_rules(freqset, supportData, minConfi=0.01):
    rules = []
    for i in range(1, len(freqset)):  # 遍历大于1的频繁项集
        for item in freqset[i]:
            subset = [frozenset([unit]) for unit in item]  # 生成项集的子集
            if i > 1:
                form_subset(item, subset, supportData, rules, minConfi)
            else:
                test_rule(item, subset, supportData, rules, minConfi)
    return rules


# 主程序部分
minSupport = 0.01  # 最小支持度
minConfi = 0.01    # 最小置信度
dataset = load_dataset('prescription.csv')  # 导入数据集
# 'groceries.csv
time_start = time.time()  # 计时
L, supportData = get_all_freqset(dataset, minSupport)  # 求频繁项集及其支持度字典
print('所有的频繁项集为：\n', L)
print('频繁项集的支持度为：\n', supportData)
print('频繁项集总数为：', len(supportData))
time_end1 = time.time()
print('求频繁项集所用时间：', time_end1-time_start, '秒')
rules = get_rules(L, supportData, minConfi)  # 挖掘关联规则
print('挖掘出的关联规则为：')
rules.sort(key=lambda x: x[2], reverse=True)

# mat = "{:^32}{:^48}{:^32}"
# print(mat.format('前件', '后件', '置信度'))
# for item in rules:
#     print(mat.format(str(list(item[0])), str(list(item[1])), item[2]))

print('关联规则总数为：', len(rules))
time_end2 = time.time()
print('求关联规则所用时间：', time_end2-time_end1, '秒')

2. 分布式Apriori代码：（distributed.py）

（以下主要为新加入的内容）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
from functools import partial  # 偏函数
from functools import reduce  # reduce需要引入 在python 3.0.0.0以后, reduce已经不在built-in function里了

# 数据集分块
def block_gen(dataset):
    blockData = []
    num = len(dataset)
    blockNum = int(sqrt(num)) + 1
    k = blockNum
    block = []
    for affair in dataset:
        if k > 0:
            block.append(affair)
            k -= 1
        else:
            block.append(affair)
            blockData.append(block)
            k = blockNum
            block = []
    blockData.append(block)
return blockData


# 统计频次的map映射函数
def map_freq(block, itemset, count):
    for affair in block:  # 遍历数据集计算候选项集频次
        for item in itemset:
            if item.issubset(affair):  # 如果候选项集是事务的子集，计数+1
                if item in count:
                    count[item] += 1
                else:
                    count[item] = 1
    return count


# 通过候选k-项集的筛选，确定频繁k-项集  ///分布式算法///
# 输入：数据集，候选k-项集，最小支持度； 输出：频繁k-项集列表，支持度字典
def get_freqset(blockData, itemset, minSupport):
    supportData = {}     # 支持度字典
    count = {}           # 计数字典
    freqset = []         # 频繁k-项集
    partial_func = partial(map_freq, itemset=itemset, count=count)
    list(map(partial_func, blockData))  # 分布式求项集频次
    number = reduce(add, map(len, blockData))  # 分布式求事务的数目
    for key in count:      # 遍历计数字典筛选符合条件的项集作为频繁项集，计算支持度
        support = count[key]/number
        if support >= minSupport:
            freqset.append(key)
            supportData[key] = support
    return freqset, supportData


# 挖掘所有满足条件的频繁项集
# 输入：数据集，最小支持度； 输出：频繁项集列表、支持度字典
def get_all_freqset(dataset, minSupport=0.001):  # 最小支持度默认0.001
    blockData = block_gen(dataset)
    C1 = get_one_itemset(dataset)
    L1, supportData = get_freqset(blockData, C1, minSupport)
    print('已经挖掘频繁', 1, '项集...')
    freqset = [L1]
    k = 0
    while len(freqset[k]) > 0:  # 循环，直到挖掘完毕所有的频繁项集（最后一项为空）
        Ck = get_itemset(freqset[k], k+2)  # 求候选项集
        Lk, support = get_freqset(blockData, Ck, minSupport)  # 求频繁项集和支持度字典
        freqset.append(Lk)
        supportData.update(support)
        k += 1
        print('已经挖掘频繁', k+1, '项集...')
return freqset, supportData

3. 事务压缩方法：（affairs_comp.py）

（主要修改部分）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# 通过候选k-项集的筛选，确定频繁k-项集
# 输入：数据集，候选k-项集，最小支持度； 输出：频繁k-项集列表，支持度字典
def get_freqset(dataset, itemset, minSupport, flag):
    supportData = {}     # 支持度字典
    count = {}           # 计数字典
    freqset = []         # 频繁k-项集
    i = 0
    for affair in dataset:  # 遍历数据集计算候选项集频次
        if not flag[i]:     # 此事务上次遍历不包含候选项集时，此次跳过
            i += 1
            continue
        flag_temp = False   # 此标记用于判断本事务此次是否包含候选项集
        for item in itemset:
            if item.issubset(affair):  # 如果候选项集是事务的子集，计数+1
                flag_temp = True
                if item in count:
                    count[item] += 1
                else:
                    count[item] = 1
        if not flag_temp:
            flag[i] = False
        i += 1
    number = len(dataset)  # 事务的数目
    for key in count:      # 遍历计数字典筛选符合条件的项集作为频繁项集，计算支持度
        support = count[key]/number
        if support >= minSupport:
            freqset.append(key)
            supportData[key] = support
return freqset, supportData


# 挖掘所有满足条件的频繁项集
# 输入：数据集，最小支持度； 输出：频繁项集列表、支持度字典
def get_all_freqset(dataset, minSupport=0.001):  # 最小支持度默认0.001
    flag = [True for _ in range(len(dataset))]  # 用于事务压缩的标记数组
    C1 = get_one_itemset(dataset)
    L1, supportData = get_freqset(dataset, C1, minSupport, flag)
    print('已经挖掘频繁', 1, '项集...')
    freqset = [L1]
    k = 0
    while len(freqset[k]) > 0:  # 循环，直到挖掘完毕所有的频繁项集（最后一项为空）
        Ck = get_itemset(freqset[k], k+2)  # 求候选项集
        Lk, support = get_freqset(dataset, Ck, minSupport, flag)  # 求频繁项集和支持度字典
        freqset.append(Lk)
        supportData.update(support)
        k += 1
        print('已经挖掘频繁', k+1, '项集...')
    return freqset, supportData

4. 爬取数据集代码：（crawler.py）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import requests
from lxml import etree
import csv
# 获取源码
html = requests.get("http://zhongyaofangji.com/all.html")
# 打印源码
print('访问成功...')
etree_html = etree.HTML(html.text)
# 获取药方链接
content = etree_html.xpath('//*[@id="divMain"]/div/div/ul/li/a/@href')
# 保存药方链接便于之后爬取
with open('url.csv', 'w', newline="", encoding='utf-8') as f:
    csv_write = csv.writer(f)
    for each in content:
        temp = [str(each)]
        csv_write.writerow(temp)
print('url保存成功...')
# 后续爬取免于从根目录爬网址，直接读取即可
# with open('url.csv', 'rt', encoding='UTF-8') as raw_data:
#     readers = csv.reader(raw_data, delimiter=',')
#     content = list(readers)
# print(content)
with open("prescription.csv", 'a', newline="", encoding="utf-8") as input_csv:
    csv_write = csv.writer(input_csv)
    num = len(content)
    for i in range(0, num):
        print('第', i+1, '项正在访问：', content[i])
        html = requests.get(content[i])
        html.encoding = 'GBK'
        etree_html = etree.HTML(html.text)
        herb = etree_html.xpath('//*[@id="divMain"]/div/div[2]/div[2]/div[2]/div[1]/p[1]/a/text()')
        csv_write.writerow(herb)
        print(herb)
本站总访问量次 | 您是第位访客