大数据作业2——k-means算法

全文共: 2.2k字   |   阅读时长: 9分
知识整理本科课程大四
  阅读

文章导航

大四上大数据分析与知识发现大作业——k-means算法

本报告主要工作：本次大作业使用python自己编程实现了k-means算法，主要介绍了算法流程，对用到的数据集进行了简要介绍，除了距离度量之外，调整不同K值情况下，衡量了聚类每一个结果簇的密度。

代码运行环境为Python 3.7.4，IDE为Pycharm，所有代码均为自己编写。参考书籍：《数据挖掘概念与技术》（原书第二版）、《机器学习实战》。

一、聚类的简要介绍

聚类：将实际或者抽象的集合组成多个类的过程。 聚类算法的常见要求有：可伸缩性、处理不同类型数据的能力、发现任意形状的能力、降噪能力、用于决定输入参数的领域知识最小化、输入顺序不敏感、高维度、基于约束聚类、可解释性和可用性等等。 它与分类最大的不同是，分类会提前指定分类数目和类别名称，聚类不会指定类别名称，甚至不会指定类别数目。不过在本次实验中的k-means算法必须指定聚类数目k，这个k被作为聚类算法中的先验知识使用。

二、算法流程

k-means算法属于无监督学习的一种聚类算法，其目的为：在不知数据所属类别及类别数量的前提下，依据数据自身所暗含的特点对数据进行聚类。对于聚类过程中类别数量k的选取，需要一定的先验知识，也可根据“类内间距小，类间间距大”（一种聚类算法的理想情况）为目标进行实现。 k-means算法以数据间的距离作为数据对象相似性度量的标准，因此选择计算数据间距离的计算方式对最后的聚类效果有显著的影响，常用计算距离的方式有：余弦距离、欧式距离、曼哈顿距离等。 本次实验中选用欧氏距离，其基本公式为：

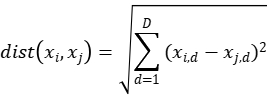
其基本算法流程伪代码为：

随机选取k个初始质心（作为初始cluster）； repeat： ——对每个样本点，计算得到距其最近的质心，将其类别标为该质心所对应的cluster； ——重新计算k个cluser对应的质心； until 质心不再发生变化

k-means存在缺点：

  • k-means是局部最优的，容易受到初始质心的影响；比如在下图中，因选择初始质心不恰当而造成次优的聚类结果（SSE较大）：
  • 同时，k值的选取也会直接影响聚类结果，最优聚类的k值应与样本数据本身的结构信息相吻合，而这种结构信息是很难去掌握，因此选取最优k值是非常困难的。

三、数据集简要介绍

UCI数据集作为一个标准测试数据集经常被用来训练机器学习的模型，广泛出现在机器学习的论文中。在此我们使用了UCI数据集中的two_cluster、three_cluster、five_cluster三个不同簇数的点集，它们都是二维数据，便于可视化观察。 为了结果变得有趣，我们还使用了真实测量的wine数据集，这些数据是对来自意大利同一地区但来自三个不同品种的葡萄酒进行化学分析的结果。分析确定了三种葡萄酒中每种所含13种成分的数量。其中13个属性分别为：

1）酒 2）苹果酸 3）灰 4）灰的碱度 5）镁 6）总酚 7）类黄酮 8）非黄酮酚 9）原花青素 10）色彩强度 11）色调 12）稀释酒的OD280 / OD315 13）脯氨酸

四、实验结果

1.two_cluster k=2

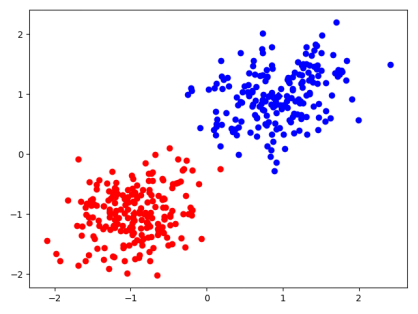
2.three_cluster k=3

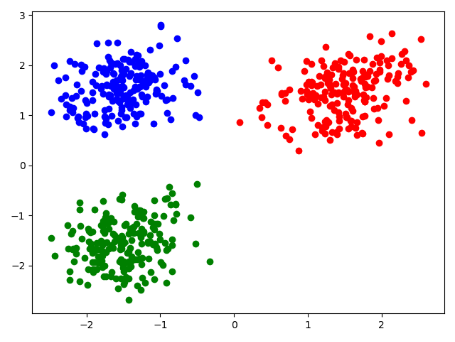
3.five_cluster k=5

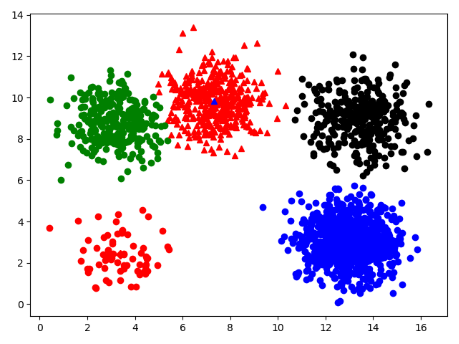
4.wine数据集 k=3

在一次测试中，迭代循环5次。

三个聚类中心点坐标为：

[1.25166667e+01 2.49420290e+00 2.28855072e+00 2.08231884e+01

9.23478261e+01 2.07072464e+00 1.75840580e+00 3.90144928e-01

1.45188406e+00 4.08695652e+00 9.41159420e-01 2.49072464e+00

4.58231884e+02]

[1.38044681e+01 1.88340426e+00 2.42617021e+00 1.70234043e+01

1.05510638e+02 2.86723404e+00 3.01425532e+00 2.85319149e-01

1.91042553e+00 5.70255319e+00 1.07829787e+00 3.11404255e+00

1.19514894e+03]

[1.29298387e+01 2.50403226e+00 2.40806452e+00 1.98903226e+01

1.03596774e+02 2.11112903e+00 1.58403226e+00 3.88387097e-01

1.50338710e+00 5.65032258e+00 8.83967742e-01 2.36548387e+00

7.28338710e+02]

都是13维向量。

（聚类结果比较庞大不便于展示，下面是部分截图）

第一列是种类编号，0~2三种；第二列是与聚类中心点的距离。

五、 调整不同k值情况下，结果簇密度

此次使用wine数据集来举例说明。

1. 轮廓系数

首先我们使用轮廓系数来衡量结果簇密度：

轮廓系数（Silhouette Coefficient），是聚类效果好坏的一种评价方式。

轮廓系数的值是介于 [-1,1] ，越趋近于1代表内聚度和分离度都相对较优。

a：某个样本与其所在簇内其他样本的平均距离

b：某个样本与其他簇样本的平均距离

则针对某个样本的轮廓系数s为：

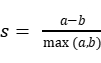
聚类总的轮廓系数SC为：

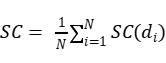
分别采用k=2，3，4，5，6来进行实验：

k 轮廓系数
2 0.6555165156460525
3 0.5711220218877621
4 0.5577126423216353
5 0.5081523788793872
6 0.5198737583976687

说明在此条件下分两类轮廓系数最大。

2.均值和方差

簇密度衡量采用以下两个指标：平均距离、距离的方差。 平均距离越大说明簇越大，方差越大说明簇密度越小 分别采用k=1，2，3，4，5来进行实验。

k 平均距离 距离方差
1 [413.72368779034764] [221.24947931661688]
2 [123.09435513723407, 157.4466947804894] [75.56317450732195, 105.68405292728465]
3 [82.69643456704392, 142.0457556870106, 68.87463704313525] [47.9537891109816, 93.6984317794299, 40.97548621196613]
4 [104.82235926873521, 59.349722824078796, 88.96909761169158, 59.98844301237363] [80.53919889877352, 35.24233250616651, 39.80030928690068, 34.23786395437574]
5 [59.01909723610794, 45.67869656758982, 48.62669527451465, 104.2003462385525, 68.32061555316555] [31.912851937637157, 22.550061590085217, 28.69038482660511, 72.61053918190882, 43.829622606222365]

从上述表格可以看出，随着k值的增大，平均距离和距离方差都在减小，这也很好理解，随着聚类粒度的减小，每个聚类簇的大小必定会有所减小，而这样就会导致每个簇中节点相似度提高，簇密度增大。

附录（源代码）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics

# 导入数据
def loadData(fileName):
    dataset = np.loadtxt(fileName)
    n = len(dataset)  # 计数，用于去除第一个值
    data = [[] for i in range(n)]
    for i in range(n):
        line = dataset[i, 1:]
        data[i] = line

    data = np.array(data)
    return data

# 计算欧式距离
def euclid(x, y):
    return np.sqrt(np.sum((x-y)**2))

# 随机生成k个聚类中心
def randomK(dataset, k):
    m, n = dataset.shape  # 获取数据集维度与个数
    centers = np.zeros((k, n))
    for i in range(k):
        centers[i, :] = dataset[np.random.randint(0, m), :]
    return centers

# k-means算法
def kmeans(dataset, k):
    m, n = dataset.shape
    mark = np.zeros((m, 2))  # 存放当前点的类别（距离最近的中心标号）与距离量
    centers = randomK(dataset, k)  # 随机生成聚类中心
    haveChange = True  # 经过一次迭代有节点所属类别有变化
    index = 0
    while haveChange:
        index += 1
        print('迭代第', index, '次')
        haveChange = False
        for i in range(m):  # 遍历每个点
            typeIndex = -1  # 当前类别
            minDis = float('inf')  # 与最近中心的距离
            for j in range(k):  # 遍历每个中心
                dis = euclid(dataset[i], centers[j])
                if dis < minDis:
                    minDis = dis
                    typeIndex = j
            mark[i, 1] = minDis  # 更新距离
            if mark[i, 0] != typeIndex:  # 如果类别有变化，更新类别
                haveChange = True
                mark[i, 0] = typeIndex
        for j in range(k):  # 更新中心
            cluster = dataset[np.nonzero(mark[:, 0] == j)[0]]
            centers[j] = np.mean(cluster, axis=0)
    return centers, mark

# 衡量每个簇的距离均值
def meanError(mark, k):
    result = [0 for i in range(k)]
    for i in range(k):
        result[i] = np.mean(mark[np.nonzero(mark[:, 0] == i)[0], 1])
    return result

# 衡量每个簇的距离方差
def stdError(mark, k):
    result = [0 for i in range(k)]
    for i in range(k):
        result[i] = np.std(mark[np.nonzero(mark[:, 0] == i)[0], 1])
    return result

# 画图展示（仅限二维）
def plotResult(dataset, centers, mark):
    m, n = dataset.shape
    k = len(centers)
    dotType = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']     # 点的类型
    centerType = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb']  # 中心类型
    if n > 2:
        print('数据大于二维，无法绘制')
        return 1
    if k > len(dotType):
        print('类别过多无法区分')
        return 1
    for i in range(m):  # 画样本点
        index = int(mark[i,0])  # 类序号
        plt.plot(dataset[i,0], dataset[i,1], dotType[index])
    for i in range(k):  # 画中心点
        plt.plot(centers[i,0], centers[i,1], centerType[i])
    plt.show()


fileName = 'wine.txt'
data = loadData(fileName)
print(data)
k = 3  # 聚类数
centers, mark = kmeans(data, k)
print(centers,'\n', mark)
plotResult(data, centers, mark)
mean_error = meanError(mark, k)
std_error = stdError(mark, k)
print(mean_error, '\n', std_error)
print("轮廓系数：", metrics.silhouette_score(data, mark[:, 0], metric='euclidean'))

# print(mark[np.nonzero(mark[:, 0] == 0)[0], 1])
本站总访问量次 | 您是第位访客