2022-08-14

生成式超图聚类：从块模型到模块化

全文共: 15.8k字 | 阅读时长: 55分

阅读

文章导航

Science Advances 2021 生成式超图聚类：从块模型到模块化。阅读报告

生成式超图聚类：从块模型到模块化

——by Zehua Ren

Chodrow P S, Veldt N, Benson A R. Generative hypergraph clustering: From blockmodels to modularity[J]. Science Advances, 2021, 7(28): eabh1303. SCIADV2021 31引用

0 摘要

提出了一种具有异构节点度和边权重的聚类超图的概率生成[1]模型，使用该模型的近似最大似然推断得到聚类目标——概括表示了当今流行的图模块度优化目标。推导出了一种推理算法，该算法推广了 Louvain 图社区检测方法，以及一种更快、更专业的变体，其中边预计完全位于集群内。使用合成和经验数据，证明了这种专门的方法具有高度可扩展性，并且可以检测基于图的方法失败的集群。在真实数据集上找到了可解释的高阶结构。

1 绪论

复杂数据中的大部分结构同时涉及两个以上实体之间的高阶交互和关系——图的推广：超图。

图聚类：通过将其节点划分为密切相关或相互关联的组（也称为集群或社区）来描述大型图。超图聚类方法在许多领域都有应用：并行计算、电路设计、图像分割、半监督学习、基因表达高阶网络分析、食物网、在线社交社区。

一种成熟的图聚类方法是将图建模为来自概率生成模型的样本，在这种情况下，聚类任务可以重铸为统计推理问题。但是现如今缺乏超图的生成技术，通常生成的超图只有一种尺寸的边，没有对节点之间的度异质性进行建模（2021年一篇解决得比较好）。边尺寸和节点度的异质性都是超图的重要特征。

有一种生成式超图聚类方法是通过连通分量扩展[2]（clique expansion）将超图转化为二元图[3]（dyadic graph），虽然这使得可以使用广泛的现有模型和算法用于图，但高阶结构丢失了，并且二元图的生成模型可能依赖于明显违反的独立性假设。

最近，已经为超图推广了基于流行的图模块化聚类目标的非生成方法，但它们缺乏与生成模型的关联，限制了它们的可解释性。——是我们之前使用的方法
生成聚类的另一种方法是将超图的表示为二分图[2]，将生成模型应用于二分图上。涉及一个强有力的假设：给定超边中任何两个节点的成员资格都是独立的，取决于模型参数。——八卦之类的交互通常只发生在受信任的个人之间。一个不请自来的局外人的存在可能会完全阻止互动的发生。这些交互的“全有或全无”（AON）结构严重违反了大多数二分生成模型所做的条件独立性假设。我们的场景也可能不适用

本文提出了一种基于度数校正的超图随机块模型[4]（DCHSBM）的超图聚类生成方法，该模型生成具有异构度分布和超边大小的聚类超图。概述了一种用于将该模型拟合到超图数据的近似坐标上升[5]最大似然估计方案，并说明该方案的一个阶段概括了经过充分研究的图模块化目标。为此类模块化目标派生了伴随的 Louvain 算法，这些目标在重要的特殊情况下具有高度可扩展性。实验表明能够在基于图的方法由于已知的理论限制而必然失败的情况下检测到集群。在具有适当匹配的高阶结构的数据集中，生成超图技术能够以比基于图的技术更高的速率恢复与元数据相关的集群。结果强调了将生成模型与数据集匹配的重要性，并指出了在高阶网络科学中进一步工作的一些方向。

2 材料和方法

2.1 DCHSBM模型

度数校正随机块模型 (DCSBM) 是具有社区结构和异构度数序列的图的生成模型。——将其推广到超图

设是超图中的节点数，每个节点被分配到个组之一，表示节点的组分配，放在向量中。与二元 DCSBM 一样，每个节点都分配有一个参数来控制其度数，放在向量中。令表示无序节点元组的集合，因此每个是一组表示可能超边位置的节点（遵循图中 DCSBM 的标准选择，我们允许包含具有重复节点的节点元组） .令表示给定元组中节点的组标签向量，而表示度参数向量。

我们使用亲和函数来控制在给定节点元组上放置超边的概率，这取决于中节点的组分类情况。形式上，将组分配映射到非负数。如果很大，则在中的节点之间形成超边的概率更高。在我们的模型中，放置在处的超边数分布为，其中表示对中的节点进行不同排序方式的数量，是度数参数的乘积。实现给定值的概率为：边生成过程的直观解释：对于中个可能的节点排序的任何一个，我们尝试在这个元组上放置符合泊松分布数量的超边。最终得到无序元组上的加权超边，其权重可以是任何非负整数。这是一个有用的建模功能，因为许多经验超图在同一组节点之间包含多个超边。即使在我们只知道是否存在超边（但不知道权重）的超图数据集中，基于泊松的模型也可以作为基于伯努利的模型在计算上的方便近似。实现给定超边集的概率就是每个上的概率的乘积。

2.2 度估计和亲和参数

在一般随机块模型 (SBM) 及其亲属中有许多推理方法：变分坐标上升、变分置信传播和马尔可夫链蒙特卡罗等。本文通过坐标上升执行近似最大似然推断。将DCSBM最大似然推断与图聚类中流行的模块化目标相结合。坐标上升框架，是块模型推理的期望最大化（EM）算法的近亲。EM算法构建“软”集群，每个节点在每个集群都有一个可能性，取最大可能；坐标上升法生成“硬”集群，其中每个节点恰好属于一个集群。轮廓似然方法（Profile likelihood methods）为最大似然推断提供了一个替代框架，可能是未来研究的方向。

在最大似然框架中，我们通过求解优化问题来学习节点标签的估计、亲和函数的估计和度参数的估计其中是由（整数加权）超边集合表示的给定数据集。像往常一样，使用具有相同局部最优值的对数似然更容易。对数似然是：其中：

第一项是对数似然取决于组分配和亲和函数的唯一部分。第二项取决于，而第三项仅取决于数据，并且可以出于推理目的而忽略。

在最大似然的坐标上升方法中，我们在两个阶段之间交替。在第一阶段，我们假设当前估计并通过求解下式得到新的和估计：结果对可以被视为最大似然估计，以标签向量的当前估计为条件。在第二阶段，我们假设当前估计 $和$ 并通过求解得到新的估计：我们在这两个阶段之间交替，直到收敛。

需要解决几个可识别性[6]问题：

首先，排列和中的组标签不会改变似然值。因此，我们对组标签施加任意顺序。
其次，可能的组数原则上可以大于中存在的组数。这种情况对应于存在统计上可能但在给定数据实现中为空的组。虽然其他处理方法是可能的，但我们选择忽略空组，将的数量等于估计中不同组的数量。
不可识别性（unidentifiability）的最终形式与和的尺度有关。对于固定的和，我们可以构造 ≠ 和 ≠ 使得（补充附录 A）。因此，为了确保可识别性，我们必须在和上设置一个联合标准化条件。我们选择约束使得：

其中并且是节点出现的超边的（加权）数。在此表达式及以下表达式中，是一个指示函数，如果其所有输入都相等，则其值为 1，否则为 0。

公式（9）的用处是，当已知或估计时，公式（7）中对和的条件最大似然估计采取简单、封闭的形式。

首先，对于固定标签向量，当使用标准化（9）时，的最大似然估计为（见补充附录 B）

其次，以为条件，如果在一些无序标签元组上取恒定值，则的最大似然估计为（见补充附录 C）

总的来说，我们可以为数据中每个可能的标签元组估计一个这样的。稍后，我们将对进行自然限制。虽然公式(10) 假设是固定的，不必知道来生成估计量。然而，通过公式(11) 生成估计量需要我们知道或估计。所以要记住 不是全局最优估计，而是以当前估计的组标签为条件的局部最优估计。

公式 (11) 也可以直接插入到完全似然最大化问题 (2) 中，消除与对应的参数并产生低维轮廓似然，原则上可以直接进行优化。这种方法对于二元块模型（普通图）是成功的，为超图块模型开发的类似方法将大有研究空间。坐标上升框架的优势在于：

我们能够通过推广常见图聚类最大似然超图Louvain算法，以开发快速启发式算法来很好地解决问题 (8) 。
在我们的框架中解决问题 (7) 也可以解释为评估固定聚类向量的轮廓似然性[7]，突出了这些方法之间的关系。

我们现在研究推断标签向量的问题。这个问题自然地引出了超图聚类的一类模块化目标。

2.3 对称模块度

上一节的结果表明，估计的度参数和分段常数亲和函数可以以封闭形式有效地估计，从而提供对的估计。这为坐标上升的第一阶段公式 (7) 提供了解决方案。我们现在讨论第二阶段公式（8）。从等式 (3)可以看出，就为了估计优化就足够了。为此，在上施加一些额外的结构是有帮助的。

我们通过规定 关于节点标签的排列对称来获得一类重要的目标函数。在这种情况下，不取决于给定节点元组中的特定标签，而仅取决于每个标签的重复次数。在统计上，相应的 DCHSBM 生成超图，其中所有组在统计上相同，取决于其组成节点的度数。因此，对称亲和函数将种植分区 SBM算法（planted partition SBM）灵活地推广到超图上。

定义函数，其中是在中的第号最大分组在本次标签向量中出现的条目数，可以任意断掉连接。例如，如果 )，则。我们称为分区向量。对称假设意味着是的函数，仅通过和它建立连接。因此，当时，我们通过定义来符号滥用[8]。

我们现在为个节点的元组定义对应于可能的分区向量的广义割（generalized cuts）和广义体积（generalized volumes）：

其中是中由个节点组成的元组子集。函数计算被分割到指定分区中的边数，而函数是诱导出分区的所有分组向量上的体积的和积。令为在大小为的集合上的划分向量集，即超边的最大大小。我们在补充附录 D 中表明，对称模块化目标可以写为：

对于个节点的元组的分区向量，直接计算是个元素的总和，当或很大时，这可能是不切实际的。不过，我们在补充附录 E 中表明，可以通过组合恒等式有效地评估这些总和。我们还给出了一个公式，用于在修改候选标签时更新体积项。

目标函数 (14) 与最近提出的多路超图切割问题相似。他们根据分割函数制定超图切割目标，当边缘在两个或多个集群之间分裂时，这些函数将进行惩罚。然后，目标是最小化惩罚的总和，约束条件为为某些节点不得位于同一集群中。我们框架中的对称亲和函数（）在其术语中对应于基于签名的分割函数。表 1 列出了许多亲和函数系列中的四个。

表 1. 对称亲和函数。在整个过程中，是分区中的节点数，和是标量，、和是任意标量函数。

亲和函数类型	公式
全有或全无 (AON)
分组数量 (GN)
相对复数 (RP)
节点对

全有或全无(AON) 亲和函数仅区分给定边是否完全包含在单个集群中。这种亲和力函数对于可扩展计算尤其重要，我们将在下面进一步讨论。
分组数量 (GN) 亲和性仅取决于边缘中包含的不同组的数量，而与每个组中的事件节点数无关。 GN 亲和函数在应用中经常出现特殊情况。当时，模块化目标的第一项对应于超边切割惩罚，在科学计算文献中称为“连通性-1(connectivity − 1)”、K-1 度量(the K–1 metric)或边界切割(boundary cut)。它在数据库文献中也被称为扇出(fanout)[9]。相关的外部度数总和惩罚也是 GN 亲和函数的一个特例。
相对复数 (RP) 亲和函数仅考虑边缘中表示的最大组的大小与下一个最大组的大小之间的相对差异。这种相当专业的亲和函数特别适用于分组大致平衡的情况，例如，我们在国会委员会的党派关系中发现。
节点对亲和函数计算边缘内分组不同的节点对的数量。虽然此亲和函数使用与二元图模型使用相似的信息，但在任何二元随机图和具有节点对亲和函数的 DCHSBM 之间没有立即明显的等价性。
还有更多对称的亲和函数；可用于定义亲和力的其他拆分函数见文献52的表三。

块模型和模块化度之间的关系最近在文献56中得到了关注。这种思考也适用于我们对上文公式(14)和下文公式(15)的推导。我们在一般的、无约束的亲和函数的假设下推导出了和的条件最大似然估计 (10) 和 (11)。当施加额外的约束——例如对称约束——时，就不能保证这些相同的估计使可能性最大化。在二元图的情况下，用于估计和的公式（10）和公式（11），在的对称假设下仅当对于每个是常数时是精确的。当组的大小不同时（这在大多数数据集中都是典型的），公式 (10) 和 (11) 是精确的条件最大似然估计的近似值。这种情况让人想起图模块化目标倾向于生成大小大致相等的分组。因此，我们在下面提出的目标函数和算法应该被理解为坐标上升最大似然推断的近似值，这仅在所有集群具有相等体积的情况下才是准确的。

2.4 AON 模块度

——全有或全无模块度

建模和计算对AON 亲和函数特别感兴趣。对于相互作用或关系的发生在很大程度上取决于组同质性的系统，这种亲和函数是一种自然选择。

将表 1 中的 AON 亲和函数插入公式 (14)，经过一些代数计算（补充附录 F），得到目标函数：

其中，集合了不依赖于分区的项。我们将和收集到向量中。我们还定义了：

在这个表达式中，是大小为的超边的（加权）个数，即。因此，切割项计算大小为的包含两个或多个不同簇中的节点的超边的数量。该计算是最近提出的图模块化方法的直接推广。我们通过限制来恢复到标准的二元模块化目标函数。我们称公式(15)是 AON 超图模块度。

最近，有研究提出了超图的“严格模块化”的优化目标函数。这种严格的模块化是公式 (15)的一个特例, 通过选择和使得和，其中是超图中所有节点度的总和。然而，保留这些参数为我们提出的 AON 目标方程 (公式15)提供了重要的灵活性。调整允许指定哪些超边大小被认为与聚类最相关。例如，在电子邮件通信中，一个非常大的收件人列表可能携带关于他们的社会关系的最少信息，并且可能需要降低大型超边的权重。调整具有修改目标函数偏爱的集群大小的效果，直接概括了二元模块化中的分辨率参数。不必事先指定这些参数的值；相反，它们可以通过公式(11)自适应地进行估计。

2.5 超图最大似然鲁汶-HMLL

为了优化模块化目标函数（14）和（15），我们提出了一系列凝聚聚类算法。这些算法通过对节点标签向量的局部更新来贪婪地改进指定的目标。这些算法的结构基于广泛使用的高性能启发式图算法： Louvain。标准启发式在两个阶段之间交替。在第一阶段，每个节点都从自己的单例集群开始。然后，每个节点被访问并移动到相邻节点的集群中，使目标的增量最大化。如果没有这样的移动增加目标，那么的标签不会改变。重复此过程，直到不存在增加目标的此类动作。在第二阶段，为每个标签形成一个“超级节点”。超级节点代表共享该标签的所有节点的集合。然后，重复第一阶段，生成更新的超级节点标签，然后在第二阶段聚合。重复该过程，直到无法再改进为止。因为第一阶段的每一步都改进了目标，所以算法以局部最优聚类向量收敛。

这种启发式可以自然地推广到超图的上。然而，异构超边大小和一般亲和函数的结合使实现变得相当复杂。

在这里，我们提供了一种高度通用的超图最大似然 Louvain (HMLL-hypergraph maximum likelihood Louvain) 算法，用于优化对称模块化目标 (14)。对于 AON 亲和函数的重要案例，简化的目标 (15) 采用了更简单、更快的专用 Louvain 算法，我们在补充附录 G 中对此进行了描述。正如我们在后续实验中所展示的，这种专用算法具有高度可扩展性，并且可以有效地恢复由 AON 亲和函数合理建模的多元结构数据集中的真实集群。

2.6 对称HMLL

我们的对称 HMLL 算法的第一阶段对映标准图上的 Louvain：节点从单例集群开始，然后贪婪地移动到相邻的集群，直到无法再增加模块度。
普通图 Louvain 的第 2 阶段以保持结构的方式将集群之间的边简化为超节点之间的加权边。然而，在超图的情况下，简单地折叠集群和超边会丢弃有关超边大小和每个超边在集群之间划分方式的重要信息。因此，在我们算法的后续阶段，我们通过移动原始超图中的整个节点集来贪婪地改进目标，而不是贪婪地移动单个节点。这样，在先前迭代中分配给同一集群的一组节点本质上被视为超级节点（supernode）并作为一个单元移动，而不会折叠超图并丢失有关超边结构的所需信息。

我们的整个过程在算法 S1 和 S2 中进行了形式化。算法 S1 依次访问上一次迭代的集群的每组节点。该算法评估与将所有移动到相邻簇时，关联的目标函数的变化量，然后执行使目标具有最大正变化的移动。重复此过程，直到移动任何一组不再能改善目标。整个对称 HMLL 方法通过算法 S2 进行总结，该算法首先将每个节点放在一个单例集群中，然后再调用算法 S1。（——S1单步，S2整体）

算法 S1 依赖于一个函数，该函数计算与将所有从中的节点移动到相邻集群后相关的目标 Q 的变化。使用组合恒等式可以有效地计算目标中第二项（体积）的变化（补充附录 E，命题 1）。对第一个（割）项的变化需要对一个节点或一组节点的所有超边求和。在每个超边，我们必须评估当前分区上的亲和性，以及与候选更新分区相关联的亲和性。这种情况与普通图 Louvain 算法的情况形成对比，在原算法中，检查给定边是否连接相同或不同集群中的节点就足够了。我们需要为每个超边存储和更新分区向量的事实阻止了我们将节点集群折叠成一个单一的超级节点，并在简化的数据结构上递归地应用算法 S2，而这在普通图 Louvain 中很常见。

因此，虽然节点集群在算法 S1 中也作为一个单元移动，但在这种情况下，有必要在算法的所有阶段对完整的邻接数据进行操作。这可以使算法 S2 在即使是中等大小的超图上也很慢。开发用于优化一般对称模块化目标或各种特殊情况的有效算法是未来工作的重要途径。

2.7 AON HMLL

当是 AON 亲和函数时，可以进行相当大的简化。对于每条边，我们不需要计算完整的分区向量，而只需检查是否成立。我们不是提供一般的亲和函数，而是提供出现在公式 (15)中的参数向量和。这使我们能够在相当简化的数据结构上进行计算。特别是，我们能够遵循经典的Louvain策略，将集群折叠成单个合并的超级节点，并将注意力限制在跨越多个超级节点的超边上。因为我们不需要跟踪超边跨越多个超节点的精确方式，所以我们可以忘记大部分原始邻接数据 ，而是简单地存储超图的边大小。这些简化既可以节省大量内存，又可以非常快速地评估目标更新函数。我们在补充附录 G 中提供了这些简化算法的伪代码。

补充附录G

上一节我们给出了通用对称亲和函数（算法 1 和 2）的超图最大似然鲁汶（HMLL）的伪代码。对于 All-Or-Nothing 亲和函数的特殊情况，可以获得相当快的 Louvain 算法。特别是，可以遵循经典的二元 Louvain 的“超级节点”策略，能够在比原始邻接超边矩阵更简单的数据结构上进行计算。算法 1 描述了 AON HMLL 的外循环。整体结构与内循环算法 2 中的大致相同。在外循环的每次迭代中，我们使用函数将初始聚类折叠成简化的超图，这种方式仍然保留了特殊的 AON 结构。我们在简化超图上运行 Louvain 步骤，然后使用函数将简化超图上的聚类转换为原始超图上的聚类。如果和重合，则 Louvain 步骤没有发现任何改进，我们终止。否则，我们开始一个新的迭代，首先在运行 Louvain 步骤之前将更新的聚类折叠成一个简化的超图。在构造简化表示时，有必要仅将折叠的超图与每个边的原始大小的向量一起存储。每个折叠节点的度数只是相应集群中节点的度数之和。

Louvain 步骤本身由算法 2 给出。在每个阶段，我们检查折叠节点并计算与将更改为时相应目标函数的变化，其中

是通过设置而其他条目保持不变获得的折叠标签向量。该计算包含在子程序中。

值得注意的是，在一般对称HMLL算法 1 中，的计算比 快得多。公式（15）中体积项的局部变化只需要更新集群体积的幂和，由分辨率参数和进行放缩。更新公式（15）的割项需要对与要更新的节点相邻的每个超边的切割状态的变化求和。在 AON 设置中，只有两种可能的状态——剪切和未剪切。检查一条边是否被切割比在可能移动之前和之后计算超边的精确分区向量要容易得多。因此，此步骤在实践中比计算对称目标的切割变化要快得多。

2.8 集群数

与大多数 Louvain 风格的模块化方法一样，用户无法直接控制 HMLL 返回的集群数量。影响聚类数量的一种方法是手动设置亲和函数或参数和的值（如果使用 AON 亲和性）。与其从数据中推断这些参数，不如先验地设置它们并在上执行一轮迭代优化获得。这种方法将二元图模块度最大化中分辨率参数的常见处理推广为调整超参数，而不是从数据中估计的数字。可能需要大量的实验来获得所需的集群数量，并且可能无法检索到确切的数量。

影响集群数量的另一种方法是在社区标签上施加贝叶斯先验。在贝叶斯方法的最简单版本中，假设在对边进行采样之前，每个节点都以相等的概率独立地分配了一个标签。实现给定标签向量的概率为，它在对数似然中生成形式为的项。该术语接下来可能会被合并到 Louvain 实现中，结果是会强烈激励减少集群总数的贪婪动作。然后，生成的正则化算法可以用稍微较少数量的不同簇来标记向量。当先验地知道数据中的真实集群数量很少时，这可能很有用。我们对 AON HMLL 的实现包含了这个可选的正则化项。我们仅在下面介绍的合成可检测性实验中使用该术语。——（？没看懂）

3 结果

3.1 运行时间

二元（Dyadic）Louvain 算法以在大图中高效而闻名。在这里，我们展示了 AON HMLL 可以在合成数据上实现与图 MLL (GMLL) 相似的性能——这是标准二元 Louvain 算法的一种变体——其中我们返回产生最高二元似然的分辨率参数和分区组合。对于固定数量的节点，我们考虑一个类似 DCHSBM 的超图模型，包含个集群和个超边——超边大小均匀分布在 2 和 4 之间。每个大小为的边以概率均匀地随机放置在同一集群内的任意个节点上。否则，以的概率，将边随机均匀地放置在任意个节点的集合上。我们使用这个模型而不是直接的 DCHSBM 来避免在每个元组节点上采样边的计算负担，这在很大时是禁止的。出于性能测试的目的，我们使用真实聚类标签计算参数向量和（在 AON HMLL 的情况下）和分辨率参数（在 GMLL 的情况下）的估计。我们强调这在实际应用中通常是不可能的，因为真实标签是未知的。我们做出这个选择是为了专注于在两种算法都能成功的情况下直接比较每种算法的运行时间。在后面的部分中，我们研究了 HMLL 和 GMLL 在亲和力和分辨率参数未知时恢复合成和经验数据中已知组的能力。

图 1 显示了当、和时在合成超图上返回的运行时间、调整兰德指数 (ARI) 和聚类数。选择这些参数以使大小为 3 和 4 的超边很少（如果有的话）完全包含在簇内。因此，不同大小的超边提供了关于真实聚类的不同信号。在这个实验中，我们通过计算标准化团投影（normalized clique projection）——连通分量扩展为普通图来实现 GMLL，其中节点通过带权重的加权二元边连接：我们还对的非标准化团投影进行了实验，但没有显示这些结果，因为在这个实验中，相关的 MLL 算法始终无法恢复与种植分区相关的标签。

根据 ARI 的测量，在较小的实例上，HMLL 在恢复种植集群方面的表现优于 GMLL。对于较大的实例，恢复结果类似。尽管 GMLL 和 HMLL 在本实验中获得了相似的准确性，但它们以不同的方式实现，HMLL 倾向于生成比 GMLL 更多、更小的集群。运行时间几乎没有区别，这表明二元团投影（连通分量扩展）对于准确性和性能都不是必需的。我们观察了参数、和的其他选择对结果的影响，其中 HMLL 在集群恢复方面的性能大大优于 GMLL，反之亦然；然而，在每种情况下，算法各自的运行时间往往只相差很小的常数因子。

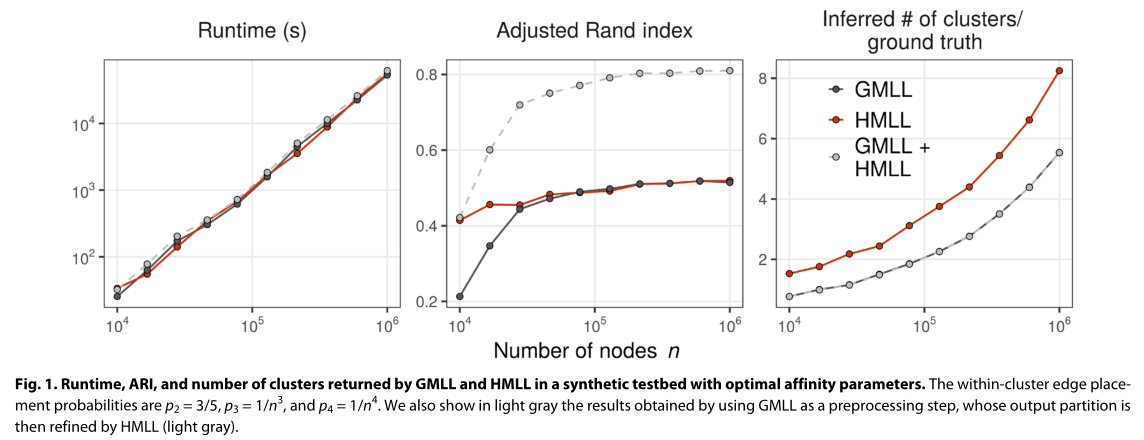
簇内边缘放置概率为，以浅灰色显示了使用 GMLL 作为预处理步骤，然后通过 HMLL细化其输出分区获得的结果。

在这个综合实验中，两种算法的组合实现了最强的恢复结果。除了独立运行每个算法之外，我们还运行了一个两阶段算法，其中使用 GMLL 生成中间分区，然后使用 HMLL 对其进行细化。我们再次强调，这些结果是在具有预先优化的亲和力参数的合成超图上获得的，因此细化策略的有效性可能无法推广到真实数据集。在下面显示的经验数据实验中，我们没有显示细化过程的结果，因为在每种情况下，组合方法的输出分区与二元方法的输出分区基本上无法区分。这可能反映了这样一个事实，即我们没有让算法先验地学习与真实数据标签相关的亲和力参数。进一步研究混合策略的性能将具有相当大的实际意义。

3.2 超图扩展（二元投影）和可检测性阈值

非正式地，当该算法的输出标记以高于零的概率与相关时，该算法能够在具有固定标签的随机图模型中检测社区。使用统计物理学的论据，文献(45) 的作者推测在图 SBM（随机块模型）中存在一个没有算法可以成功检测社区的机制。这个猜想后来在各种特殊情况下得到了提炼和证明；参见文献 (61) 的综述。在具有两个相等大小的种植群落的二元 SBM 中，大图中可检测性的必要性限制条件是：其中是连接到节点的簇内边的平均数，而是连接到节点的簇间边的平均数。如果不满足此条件，则没有算法可以可靠地检测关联图 SBM 中的社区，尽管社区在统计上是不同的。该界限限制了直接推理方法，例如贝叶斯或最大似然技术，以及基于模块化或其他图目标函数最大化的方法。最近的几篇论文考虑了均匀超图的可检测性问题。在我们的模型中，存在多种尺寸的边使分析变得复杂。在这里，我们将自己限制在一个实验证明中，即图 SBM 和我们的 DCHSBM 的可检测性机制可能存在显着差异。

图 2 显示了在一个简单的 DCHSBM 上进行的两个实验，其中有两个大小相等的社区，每个社区有 250 个节点。对亲和力进行了调整，使得：

每个节点平均与 5 个 2 节点边和 5 个 3 节点边相关。
2 节点边的一部分连接同一集群中的节点，而 2 节点边的一部分连接不同集群中的节点。
3 节点边的一部分连接同一集群中的节点，而 3 节点边的一部分连接不同集群中的节点。

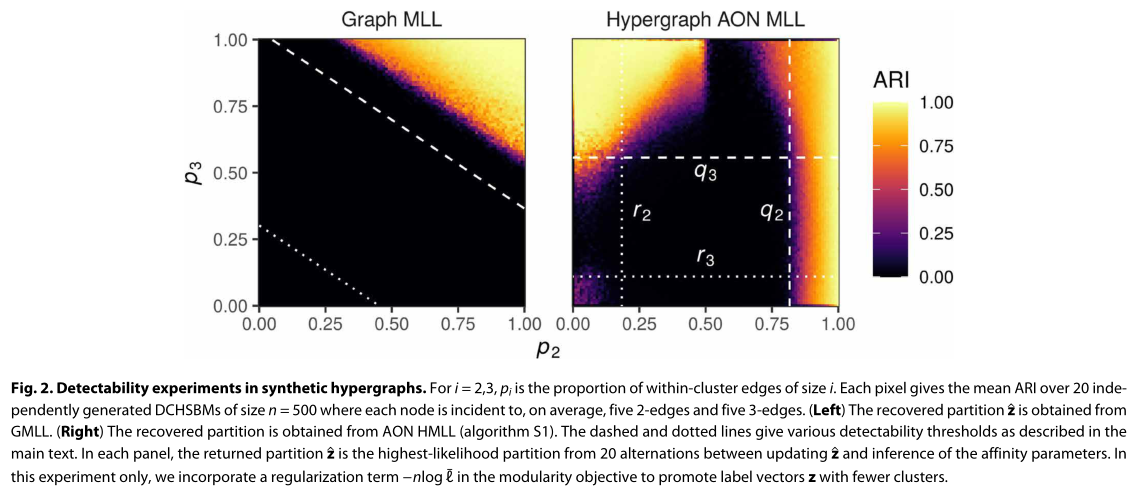
对于* ，是大小为 i 的簇内边缘的比例。每个像素给出 20 个独立生成的大小为 n = 500 的 DCHSBM 的平均 ARI，其中每个节点平均与 5 个 2节点边和 5 个 3节点边发生关联。（左）从 GMLL 获得恢复的分区。（右）从 AON HMLL（算法 S1）获得恢复的分区。虚线和点线给出了正文中描述的各种可检测性阈值。在每个面板中，返回的分区是在更新和相似性参数推断之间的 20 次交替中的最高似然分区。仅在这个实验中，我们在模块化目标中加入了一个正则化项，以促进生成具有更少簇的标签向量。

这部分看不懂

仅在这个实验中，下面讨论的 GMLL 和 AON HMLL 都在似然目标中使用贝叶斯正则化项，以促使每个算法形成相对较少数量的集群。在左侧面板中，我们展示了使用 GMLL 的非标准化变体时返回的分区与真实分区的 ARI（标准化变体的结果相似）。这种选择反映了这样一个事实，即真实的簇数是已知的并且等于 2。白虚线和白点线给出了等式(18)成立的边界。白虚线给出了分类机制的可检测性阈值，其中节点更有可能与同一集群中的其他节点链接。 Louvain 作为一种聚类算法，非常适合检测分类簇，并且能够在该机制的大部分（但不是全部）中检测社区。理论阈值与 Louvain 性能之间的差距反映了 Louvain 作为一个阶段性贪心算法没有最优性保证的事实。在白点线下方还有一个不可检测的区域。基于图的 Louvain 的凝聚结构导致算法在这里完全失败。

在右侧面板中，我们展示了使用 AON HMLL 的相同实验。虚线和分别给出了完全忽略 3 节点边和 2 节点边的假设算法的分类可检测性阈值，而点线和给出了相应的不可检测阈值。 HMLL 能够检测种植分区的一系列参数值，而 GMLL 不能。其中包括某些大小的边主要位于簇间的情况，如左上角（小）和右下角（小）所示。有一个机制（中和右下），其中算法似乎受到边界 q2 的约束，这表明 HMLL 有效地忽略了该机制中的 3 节点边。然而，随着的增加，3 节点边变得更具信息性，并且可以在的分区（右上角）检测到某些值。还有一个广泛的机制（左上角），其中超图算法能够有效地使用 2 节点和 3 节点边来检测集群，即使 2 节点边主要在集群之间。我们还观察到 HMLL 在 2 边和 3 边都在簇间（左下）的情况下检测簇的能力非常有限。因为 HMLL 又是一种凝聚算法，所以它对诸如此类的完全不分类分区的性能充其量是不可靠的。

有趣的是，还有和的组合，其中 GMLL 能够检测到种植分区，而 HMLL 则不能。这可能表明二元投影所暗示的不同大小的边的汇集在某些情况下可能是有用的。我们再次注意到 GMLL 和 HMLL 都不是最优推理算法。最佳超图算法可能会显着扩展图 2 右侧面板中的可检测范围。我们将这些算法的开发及其分析视为未来研究的极有希望的途径。

3.3 经验数据上的实验

接下来，我们分析了从经验数据中得出的几个超图。

前两个是人类近距离接触交互的超图，从小学和高中的可穿戴传感器数据中获得。节点是学生或老师，超边连接彼此靠近的人群。节点标签标识每个学生所属的班级，小学数据还包括与每个班级关联的老师。
接下来，我们从美国国会法案共同提案数据中创建了两个超图，其中节点对应于国会议员，超边对应于众议院或参议院法案的发起人和所有共同发起人。
我们以委员会成员的形式从美国国会构建了另一对数据集。每条边都是国会会议中的一个委员会，每个节点又对应于众议院议员或参议员。如果相应的立法者在指定的国会会议期间是委员会成员，则节点包含在边中。包含了跨越 1993 年至 2017 年从第 103 届至第 115 届的所有国会议员。众议院和参议院成员仍然有单独的数据集。在所有国会数据集中，节点标签给出了成员的政党。
我们还使用了沃尔玛购买的超图，其中每个节点都是一个产品，超边连接了客户在一次购物之旅中共同购买的一组产品。每个节点都有一个关联的产品类别标签。
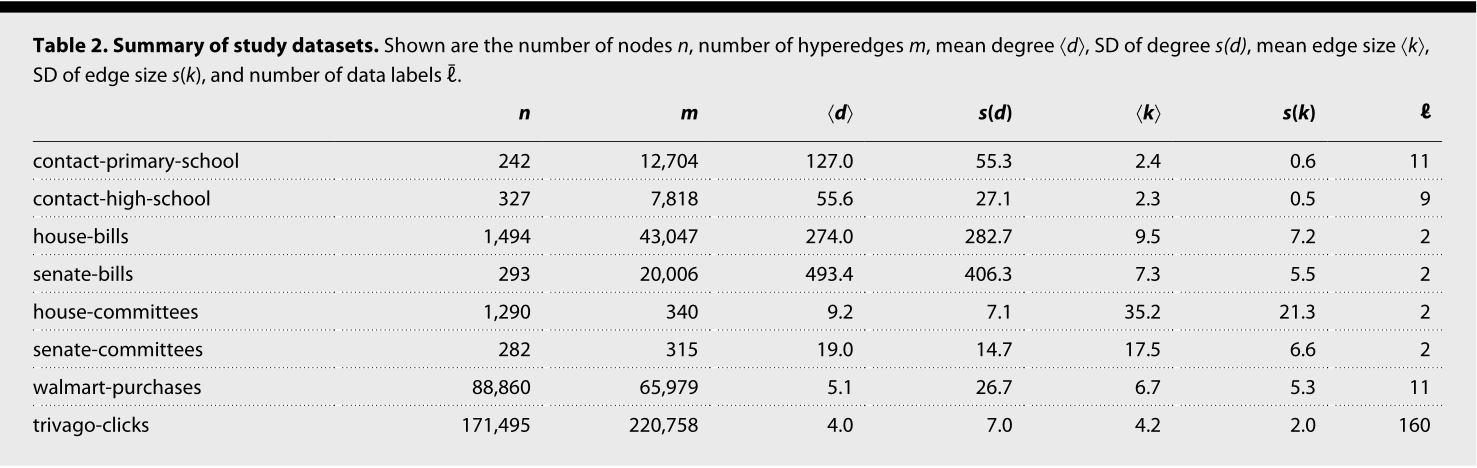
最后，我们构建了一个超图，其中节点对应于 trivago.com 上列出的酒店，每个超边对应于一组酒店，其网站被 Trivago 的用户在浏览会话中点击。该超图源自 2019 年 ACM RecSys 挑战赛发布的数据。对于每家酒店，节点标签给出了它所在的国家/地区。数据集的大小在节点数量、超边、超边大小和节点标签方面有所不同（表 2）。

表2. 研究数据集摘要。显示了节点数、超边数、平均度、度数的标准差、平均边大小、边大小的标准差和数据的标签数 .

数据集
contact-primary-school	242	12704	127.0	55.3	2.4	0.6	11
contact-high-school	327	7818	55.6	27.1	2.3	0.5	9
house-bills	1494	43047	274.0	282.7	9.5	7.2	2
senate-bills	293	20006	493.4	406.3	7.3	5.5	2
house-committees	1290	340	9.2	7.1	35.2	21.3	2
senate-committees	282	315	19.0	14.7	17.5	6.6	2
walmart-purchases	88860	65979	5.1	26.7	6.7	5.3	11
trivago-clicks	171495	220758	4.0	7.0	4.2	2.0	160

3.4 模型比较和高阶结构

人们经常说，高阶特征对于理解复杂网络的结构和功能很重要。但很少有人能说清哪些类型的高阶特征与哪些网络相关。生成式建模提供了一种比较不同类型的高阶结构的方法。在 DCHSBM 中，此结构由亲和函数指定。比较每个亲和度函数的似然函数可以表明哪一个最有可能作为基础数据的高阶生成机制。我们使用表 1 中的对称亲和函数和上述节点的标签进行了比较。在这个比较中，我们可以计算亲和函数的近似 ML（最大似然）估计并给定它的函数形式。为了进行具体的比较，有必要指定 GN、RP 和 Pairwise 亲和度的函数形式。我们使用以下公式给出：

GN 亲和力函数为超边大小和组数的每个组合分配一个单独的参数。
RP 亲和性函数为边内最大和第二大组之间的差异超过 k/4 的情况分配一个参数，其中 k 是边的大小。
Pairwise 亲和性函数将一个参数分配给不同组中的二元对的总数超过这些对的可能数量的一半的情况。

RP 偏爱两个最常见的标签在表示上大致平衡的超边；
而 AON、GN 和 Pairwise 都偏爱具有同质聚类标签的超边。

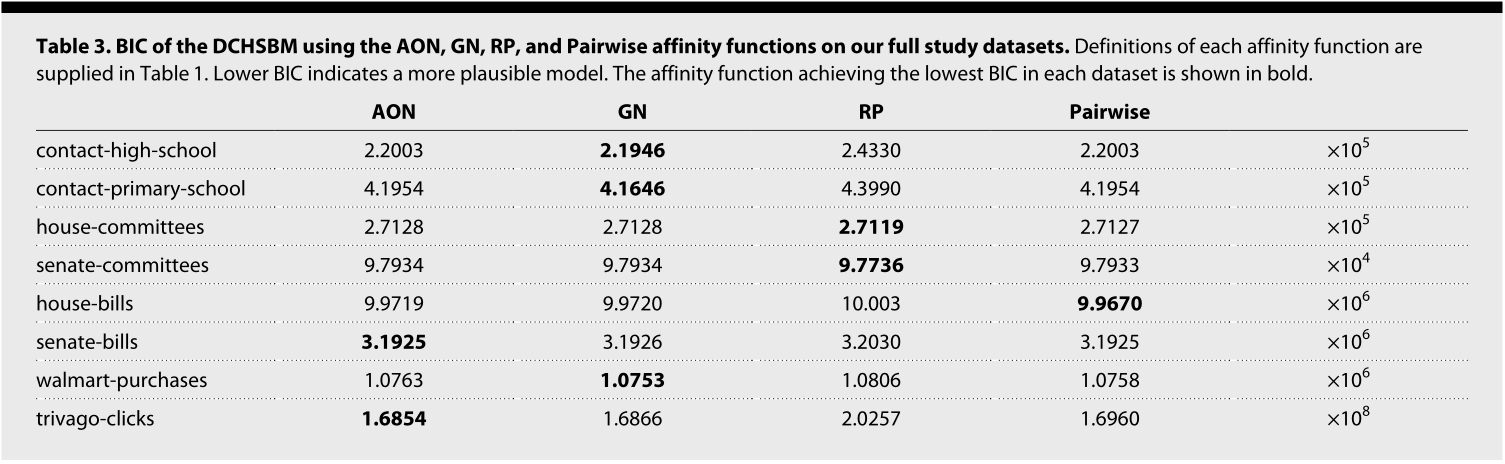
因为这些亲和函数参数的数量不同，我们通过贝叶斯信息准则[10] (BIC) 对它们进行比较，该标准会惩罚具有比数据支持的更多参数的亲和函数。在计算 BIC 时，我们排除了节点数量的参数，因为此参数在每个模型中都是相同的，反而增加了一个不重要的加性常数。 AON、RP 和 Pairwise 亲和度各有个参数。在 GN 的情况下，我们通过使用给定分区方案中不同标签的数量计算可能组的数量，来计算每个边大小的可能参数的数量。例如，如果给定的分区仅包含三个不同的组，那么我们不会设置与包含三个以上组的边相对应的参数。移除这个限制也是合理的，在这种情况下，大小为的边将有个参数，而与无关。

表 3 显示了使用这些亲和函数中的每一个的 DCHSBM 的 BIC。在所有研究数据集中，没有一个亲和函数是首选的，这表明存在不同种类的多元结构。在两个国会委员会数据集中，RP 实现了最佳 BIC，而在其他每个数据集中，促进边缘同质性的三个亲和力之一反而是首选。这三种亲和力之间也有重要的区别。在 house-bills 中，Pairwise 亲和度函数总体上实现了最低的 BIC，而在 walmart-purchas 中，Pairwise 亲和度优于除 GN 亲和度之外的所有功能。这表明仅涉及节点标签的成对比较模型这些情况下可以对数据提供相对强的生成解释。反过来，这表明二元算法在这些二元数据集上的性能至少与其多元算法一样好。正如我们将在下面看到的，在这两个数据集中，与 AON HMLL 返回的聚类相比，二元算法可以返回与真实结果更相关的聚类。

表 3. 在我们的完整研究数据集上使用 AON、GN、RP 和 Pairwise 等亲和函数运行DCHSBM 的 BIC 。表 1 中提供了每个亲和函数的定义。较低的 BIC 表示更合理的模型。在每个数据集中实现最低 BIC 的亲和函数以粗体显示。

数据集	AON	GN	RP	Parwise
contact-high-school	2.2003	2.1946	2.4330	2.2003	×10 5
contact-primary-school	4.1954	4.1646	4.3990	4.1954	×10 5
house-committees	2.7128	2.7128	2.7119	2.7127	×10 5
senate-committees	9.7934	9.7934	9.7736	9.7933	×10 4
house-bills	9.9719	9.9720	10.003	9.9670	×10 6
senate-bills	3.1925	3.1926	3.2030	3.1925	×10 6
walmart-purchases	1.0763	1.0753	1.0806	1.0758	×10 6
trivago-clicks	1.6854	1.6866	2.0257	1.6960	×10 8

3.5 在关系超图中发现类别

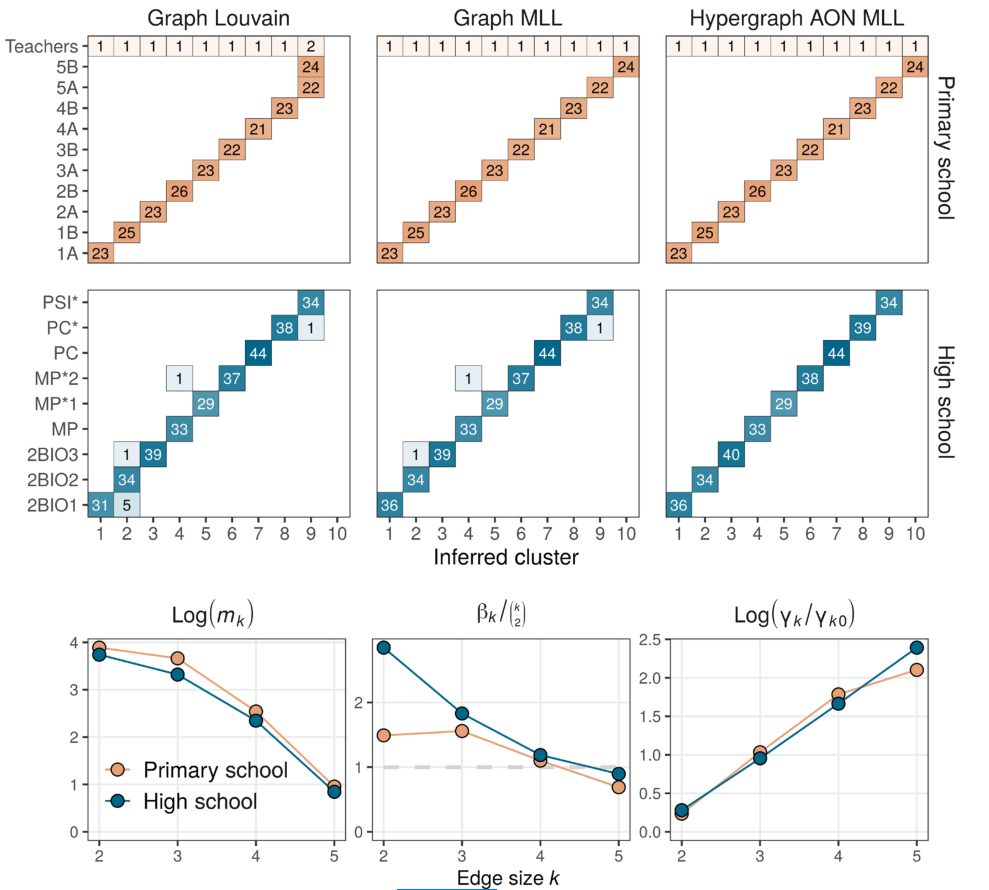
图 3 小学和高中数据集的聚类算法比较。对于每个数据集，我们对比了从经典图 Louvain 模块化最大化启发式获得的分区、从 GMLL 获得的分区和通过 AON HMLL 获得的分区。显示的分区是经过 20 轮迭代似然最大化后获得相应目标函数的分区。每个框记录具有推断集群和真实标签的指定组合的代理数量。底行可视化大小为的边数、推断的大小权重和推断的分辨率参数，如公式 (15) 中定义。在最右边，。

为了测试 AON HMLL 算法本身，我们首先研究它在小学和高中网络中的行为。表 3 中 BIC 分数的比较表明，GN 可能是对数据最具解释性的模型，但我们改为使用 AON 来利用其可观的计算优势。我们在 AON HMLL 和 AON 参数估计之间执行了 20 次交替，并返回了具有最高 DCHSBM 可能性的分区。我们将结果与两种二元方法进行比较。 Graph Louvain 算法的每个步骤在使用标准 Louvain 算法推断集群和使用的近似最大似然框架估计分辨率参数之间交替进行。 Graph Louvain 返回最大化经典二元模块化目标的分区。我们还与 GMLL 进行了比较，后者执行相同的交替，但返回的分区使相应的种植分区 SBM 的近似对数似然最大化。

图 3 比较了每种算法的性能。

在小学数据集的情况下，我们认为基本事实分区是为每个班级准确分配一名教师的分区。 Graph Louvain 能够找到与给定班级标签具有明确相关性的学生分区，但却会将两个小学班级合并，拆分了几个高中班级（左列，前两行）。GMLL 能够完美地恢复小学生的班级标签，对三个高中生进行错误分类。我们提出的 AON HMLL 能够正确恢复两个数据集中的给定分区。

通过研究推断的亲和函数的结构，我们可以获得对 HMLL 行为的一些定性洞察。最直观的方法是通过从公式15导出的参数和。图 3 的底行显示了这些参数和边缘尺寸的分布。对边大小的依赖性提供了为什么 GMLL 在接触小学成功但在接触高中犯了几个错误的一种解释。在标准二元投影下，k-超边生成个2节点边，因此多次出现在二元模块化目标。在小学数据集的情况下，估计的重要性参数确实比较接近（图 3，底部中间）。因此，在最佳分割处，边缘的相对权重因团投影而失真相对较小。另一方面，高中数据集的估计值与有很大的偏差，尤其是在时。在这里，小边在多元模块化目标中的特征比在投影二元目标中更突出，这意味着后者在最优分区附近对前者的逼近较差。这种差异可以解释接触高中 GMLL 中的小错误。图 3 的右下图将特定尺寸分辨率参数的推断值与进行比较，后者是 (40) 中使用的隐含值。推断的分辨率参数始终较大并随增加，突出了在我们的方法中自适应估计这些参数的价值。

3.6 具有大超边的集群恢复

在图 4 中，我们研究了 AON HMLL 在我们的多个研究数据集中恢复真实社区的能力。与这两个接触网络不同，这些数据集中的每一个都包含大小高达 25 个节点的边。我们排除了众议院委员会和参议院委员会，理由是这些数据集是不相关的，这表明 AON 显然不合适。我们将 AON HMLL 与 GMLL 的两个变体进行比较。在非归一化变体中，我们通过将每个边替换为团块（k-clique）来获得一个二元图，从而生成总共个二进边。在归一化变体中，我们将 k-clique 中的每条边加权为的因子。然后每个节点的归一化二元图的度等于其在原始超图中的度。在任何一种情况下，我们都会在用于估计聚类的二元 Louvain 算法和分辨率参数的条件最大似然推断之间交替。在每次试验中，我们对 AON HMLL 和两个 GMLL 变体执行 20 次迭代，从这些变体中返回达到最高可能性的组标签和参数的组合。然后，我们通过 ARI 将聚类与真实标签进行比较。我们改变最大边缘大小以显示每个算法如何响应逐渐变大的边缘的合并。因为极端稀疏性通常会给社区检测算法带来问题，我们展示了针对 trivago-clicks 和 walmart-purchases 的逐渐密集核心的实验。超图的核被定义为最大的子超图，使得中的所有节点都具有至少的度数。

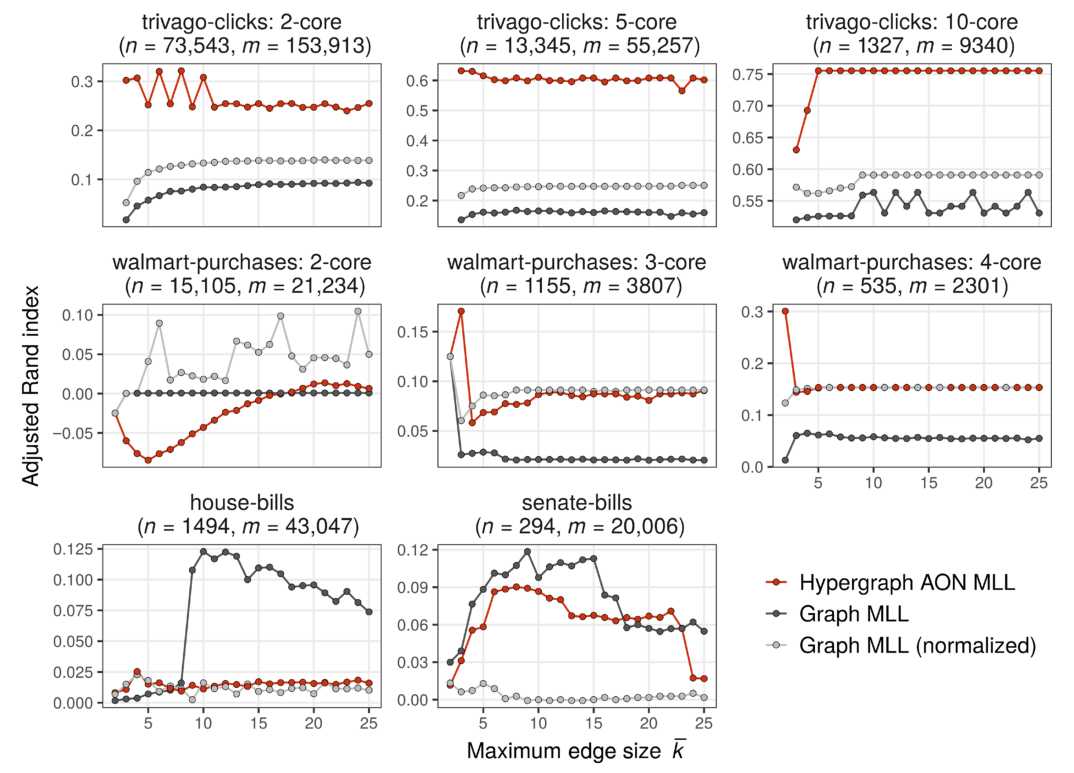
图 4. 具有已知聚类的数据中超图 AON MLL（算法 S1）与二元似然 Louvain 的比较。点给出了在分区和参数估计之间进行 20 次交替后获得的最高似然分区的 ARI。最大超边尺寸沿水平轴变化。在面板标题中，是节点数，是时的边数。请注意，垂直轴限制因面板而异。

结果突出了 AON HMLL 的性能对作为数据生成机制的 AON 亲和函数的相对合理性的强烈依赖性（参见表 3）。在 trivago-clicks 中，AON 亲和函数达到了所有四个候选者中最低的 BIC。因为 AON 是一个更合理的生成机制，所以 AON HMLL 能够找到与提供的数据标签相关的分区比二元变体返回的分区更相关，这并不罕见。另一方面，在沃尔玛购买中，Pairwise 亲和力优于 AON。在这种情况下，AON HMLL 的性能要差得多，并且在 2 核中，甚至返回与提供的标签反相关的集群。随着弱连接节点被移除并且生成的数据变得更密集，HMLL 开始返回相关集群。然而，归一化的 GMLL 变体在恢复数据标签方面至少同样有效。在两个国会法案数据集中，Pairwise 亲和力在众议院实现了低于 AON 的 BIC，在参议院实现了可比的 BIC。与这一发现相呼应的是，二元法在每种情况下都优于 AON HMLL。非标准化的 GMLL 在众议院和参议院的法案中表现最好，而标准化的 GMLL 在沃尔玛采购中更受欢迎。此外，HMLL 是仅在 walmart-purchases 小的 2 核的情况下最差的算法。因此，在不知道归一化或非归一化二元表示是否更适合数据的情况下，HMLL 可能是首选算法。

在解释这些恢复结果时，重要的是要将它们与社区检测方法的一般局限性和特别是模块度最大化的局限性联系起来。没有对数据结构做出隐含假设的社区检测“最佳算法”，算法与数据集的不匹配会产生误导性结果。即使数据生成过程确实与算法假设相匹配——例如从 SBM 生成的合成数据集——最优算法也可能由于稀疏性而无法检测到种植群落。贪婪的模块化最大化，包括这里考虑的 Louvain 变体，只能找到可能的许多局部最优值之一，其中一些可能在很大程度上彼此不相关。这些考虑意味着：

（i）我们不能排除可能在三种算法中的任何一种中获得更高分数的其他局部最优值的存在，以及
（ii）算法无法恢复接近基本事实的聚类这一事实并不意味着它在其既定目标（即局部似然最大化）中“失败”了。

总体而言，我们的结果表明，当具有 AON 亲和函数的 DCHSBM 假设适用于数据时，AON HMLL 在恢复真实社区方面的表现优于二元方法。在实践中，因为我们通常无法访问基本事实标签，所以假设是否适合数据的问题应该由领域专业知识来告知。

4 讨论

我们提出了一种基于 DCHSBM 的多元数据聚类生成方法。从这个模型中，我们推导出了一个对称的、类似模块化的目标，其中包括 AON 模块化目标作为一个重要的特例。这种推导将超图模块化目标与具体的建模假设联系起来，可以根据领域专业知识进行调整。我们还制定了类似 Louvain 的算法来优化这些目标，在 AON 亲和函数的情况下具有高度可扩展性。将这种启发式嵌入到交替近似最大似然方案中，可以对节点集群和亲和性参数进行自适应估计。我们已经通过实验证明，超图算法与二元算法具有明显不同的可检测性机制。我们还对经验数据进行了实验，发现在建模假设有充分根据的数据集中，超图方法优于二元法。

我们的工作指向了许多进一步研究的方向。这些方向之一是算法。我们在 DCHSBM 中进行推理的贪心坐标上升框架有几个重要的限制。

首先，因为我们依赖于一个 NP-hard 优化步骤，所以永远无法保证似然的全局最大化。
其次，即使是精确的最大似然本身也被限制为推理范式，因为它使用的信息仅包含在似然图的一小部分中。我们的方法，作为仅当集群大小大致相等时才准确的近似值，也可能会受到估计偏差的影响。
第三，由 Louvain 风格算法体现的边缘凝聚方法在适用促进边缘内同质性的亲和函数（那三种）方面受到限制。

替代推理范式可以改善部分或全部这些限制。

在最大似然推断的框架内，直接最大化轮廓似然为坐标上升提供了一个有趣的替代方案。尽管所有最大似然方法在优化相同的目标函数方面都是等价的，但算法属性（例如运行时间和陷入不良局部最优值的倾向）可能因不同方法而异。
完全贝叶斯处理提供了另一条有希望的途径，尽管它们有时在计算可扩展性方面受到限制。
变分置信传播提供了一个有趣的折衷方案，实现了相当大的可扩展性以换取几个近似值。
最近的工作在这个方向上取得了进展，但与非均匀超图的可扩展性和行为相关的几个问题仍然存在。具有更一般的亲和力函数的可扩展推理的信念传播方法将具有特别的实际意义。

还有几个重要的理论发展方向。其中之一是 DCHSBM 中的可检测性问题。由于 DCHSBM 比二元 DCSBM 更灵活，因此该模型中的可探测性理论可能要复杂得多。另一个方向涉及扩展到此处讨论的超图模块化目标的二元模块化目标的属性。除了作为与空模型比较的作用和作为 DCSBM 似然性中的一个术语外，二元模性还表达了图上扩散过程的稳定性和定义的离散表面张力的能量图表。这些属性的扩展，或者解释它们为什么不能概括，对理论家和实践者都有帮助。

附注

1 生成vs.判别

帖子：生成方法vs判别方法+生成模型vs判别模型

生成模型：能够随机生成观测数据的模型，可以用来直接对数据建模。

与判别模型区别：生成模型，就是同时考虑了X和Y的随机性，也就是说二者都是随机变量；判别模型，就是只考虑了Y的随机性，而X并不是个随机变量，即使X存在于条件中，但是并没有p(x)这种说法。

生成模型有三个基本用处：一个是概率密度估计，一个是采样，还有就是监督学习，如朴素贝叶斯。

2 超图的两种扩展方式

clique expansion（连通分量扩展）

将超边中所有顶点都连接在一起，比如有3个顶点的超边，扩展成普通图时两两相连就会有3条边。以此类推。连接和n个顶点的超边拓展后有个边。同一个超边转换成的边具有跟以前边同样的权重。
star expansion（星形扩展）

在每个超边中加入一个“星星”,连接上其他的点，所以这种方式会在原来的节点上增加额外的节点，也就是有加点的操作，而法一是没有的。加上的点归入一个集合，原来的点归入另一个集合，这个拓展后的普通图是一个二部图（bipartite graph又称作二分图，是图论中的一种特殊模型。）

星图边的权重变成对应超边的权重除以超边的度。