【复杂网络】绪论

文章导航

× 文章目录

1. 1. 研究领域
2. 2. 本课程涉及的内容
   1. 2.1. 拓扑数据分析：UMAP
   2. 2.2. ECG：图上的集成聚类
3. 3. 总目录

菲尔兹数学科学研究所 复杂网络2019夏令营课程 学习笔记

菲尔兹数学科学研究所 复杂网络2019夏令营课程

授课老师来自：Tutte数学与计算研究所 ——加拿大政府研究机构，成立于2011年

基于Python3、igraph框架。2019.8 ComplexNetworks2019

本夏令营的其它课程资料（Julia）：

day1day2

day3day4day5

研究领域

1. 密码学
   • 经典密码学
   • 后量子公钥密码学
   • “高级密码学”
2. 数据科学
   • 机器学习理论与实践
   • 图挖掘技术
   • 网络防御和安全应用
3. 脆弱性研究
   • GC系统的网络安全
   • 流水线

本课程涉及的内容

1. UMAP：统一流形逼近和投影——是一种降维技术，可用于类似于 t-SNE 的可视化，但也可用于一般的非线性降维。UMAP 是一种基于流形学习技术和拓扑数据分析思想的降维算法。它为处理流形学习和降维提供了一个非常通用的框架，但也可以提供具体的具体实现。
2. 图聚类（Graph clustering）：各算法比较，一种新算法（ECG）
3. 图嵌入（Graph embedding）
4. 图上的半监督学习
5. 超图模块化和聚类

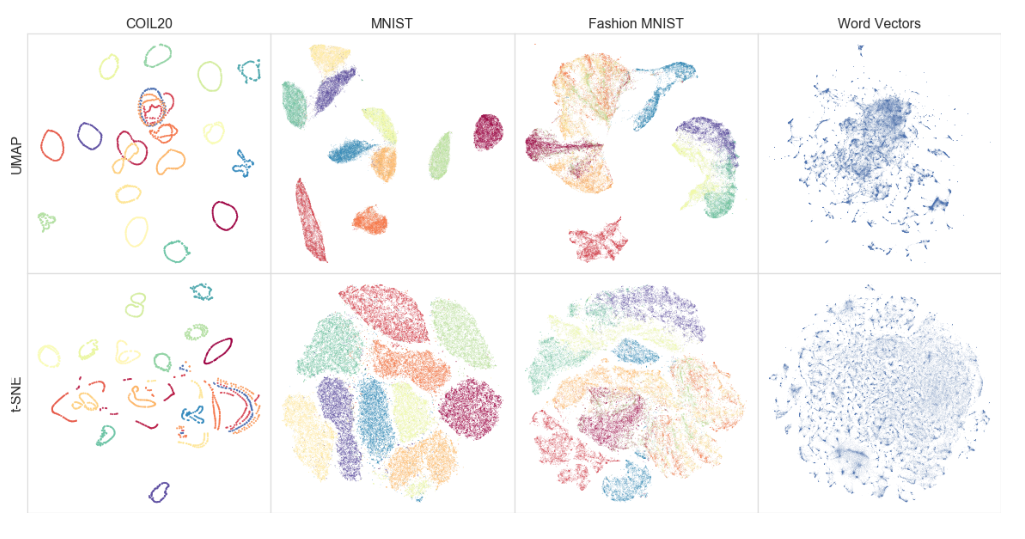
拓扑数据分析：UMAP

1. 降维技术
2. 范畴论（Utilizes category）和代数拓扑学（algebraic topology）的使用
3. 真实应用

和t-SNE算法的对比

t-SNE是一种非线性降维算法，非常适用于高维数据降维到 2 维或者 3 维，进行可视化。在实际应用中，t-SNE很少用于降维，主要用于可视化

ECG：图上的集成聚类

——Ensemble Clustering on Graphs

总目录

1. 关系数据挖掘
   • 中心性度量
   • 图模型
   • 基准（benchmarks）
2. 社区结构
   • 图划分（graph partitions）算法比较
   • 图聚类算法
   • 图上的集成聚类（ECG）
3. 图嵌入
4. 图上的半监督学习
5. 超图模块化和聚类