【复杂网络】关系型数据挖掘

文章导航

× 文章目录

1. 1. 关系型数据
   1. 1.1. 术语
   2. 1.2. 关系型数据
   3. 1.3. Issues
   4. 1.4. Problems
2. 2. 中心性
   1. 2.1. 度中心性
   2. 2.2. 节点中心性
   3. 2.3. 边中心性
   4. 2.4. 相关性
3. 3. 图模型（随机图）
   1. 3.1. ER模型
   2. 3.2. CL模型
      1. 3.2.1. 伯努利Chung-Lu模型
      2. 3.2.2. O(m) Chung-Lu模型
   3. 3.3. 配置模型（Degree Sequence）
4. 4. 基准（小世界 幂律）
   1. 4.1. 小世界网络
   2. 4.2. 聚类系数
   3. 4.3. 幂律网络
   4. 4.4. BA网络（Barabasi-Albert）

菲尔兹数学科学研究所 复杂网络2019夏令营课程 学习笔记

关系型数据挖掘（Relational data mining）

• 中心性度量
• 图模型
• 基准（benchmarks）

简介：使用jupyter notebook、python3、igraph包

关系型数据

术语

1. 监督学习：分类（classification）、回归（regression）
2. 无监督学习：聚类（clustering）、密度估计（density estimation）、降维（dimension reduction）、异常值检测（outlier detection）。
3. 半监督学习：标记的数据很少，同时使用标记和未标记的数据

• 特征：feature（连续、分类或排序）

关系型数据

实体表示为点，关系可以表示为边，或超边（是否加权、是否有向）

• A和B是朋友
• A给B发邮件
• A，B和C在同一个团队

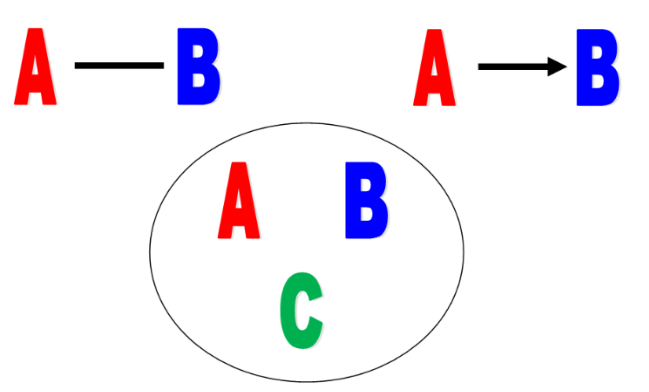
关系型数据被建模为图（graphs）或超图（hypergraphs）

, let and ——得到邻接矩阵（一些性质，不再赘述）

完全图（Complete graph），也叫集团（clique）

---

图会出现在不同场景中：电子邮件交换、蛋白质-蛋白质相互作用图、社交关系（空手道俱乐部）、赛事（大学足球队之间的比赛）

Issues

一个图里面有很多社区，传统机器学习将向量空间进行嵌入降维后可以进行聚类。

有许多工具可以处理这些数据，抽样等统计技术可用于处理大型数据集。

采样保留关键属性（簇、平均距离等），但这些都在图形空间中被破坏。

Problems

1. 中心性度量
2. 寻找社区
3. 异常检测
4. 种子集扩展（seed set expansion）-局部采样
5. 链路（边缘）预测
6. 半监督学习
7. 向量空间嵌入

中心性

度中心性

所有边权值之和

入度、出度：入边权值和、出边权值和

归一化度中心性：无权图（出入）度除以来获得（假设没有自环）

节点中心性

中心性（Centrality）：综合考虑节点度和连接到高度数中心的其他节点 ，唯一解为——连通图无定义，需要进行扩充定义

• 定义一：特征向量中心性（eigenvector centrality）

  将特征向量中心性定义为与（neighbour’s centrality）成比例

  节点i的特征向量中心性是以下方程的解： 有向图，入度和出度分别进行定义

  对于连通图，我们测量与最大特征值相对应的特征向量的中心性，最大特征值是实的和正的（Perron Frobenius），即： u1是主导特征向量

• 定义二：接近中心性（closeness centrality）

  考虑节点之间的最短路径（最小跳数或最小边权重之和）——测地线（geodesic） dij为最短路径长度，dii=0，不可达定义为无穷，无权图可定义为节点数n

• 定义三：介数中心性（betweenness centrality）

  更常用的方法是考虑所有测地线：

  • 定义为节点j和k之间所有的测地线的数量
  • 定义为节点j和k之间通过节点i的测地线的数量

• 定义四：Δ中心性（delta-centrality）

  考虑从G中删除某些节点i的影响

  • 设P(G)是图G上性能的一些度量
  • 设Gi是通过从图G移除与节点i相邻的所有边而获得的图

  ——注意，我们要保证

  • 一种可能的P(G)取值：定义图G的影响力E(G)——

  说明：

  • 对于不连通图，dij=∞的节点对的贡献为零。
  • 通过考虑节点集，所有中心性度量都可以推广到组中心性度量。——节点集的度定义为非g节点连接到g内节点的数量

• 定义五：谷歌PageRank算法中使用的中心性

  思想：互联网中重要页面与许多重要页面相互链接

  • 我们在节点i处随机游走：

    • 以概率：跳到随机节点。
    • 以概率：以概率跳到节点j。
    • 可以用代数或迭代（幂）方法获得PageRank值的解

  • 在有向图中，我们将中枢（hub）定义为具有高出度的节点，而将权威（authority）定义为具有高度入度的节点。

  • 在无向图中，这两个概念是相同的。

• 定义六：中枢/权威中心性（hub/ authority）

  中枢中心性： 权威中心性： 让，我们有：

边中心性

• ：节点j和k之间的测地线数
• ：通过边e的节点j和k之间的测地线数。

相关性

基础知识：

• 设pi为出现次数为i次的节点在G中的比例，即度分布
• 度相关性 度量 由边链接的节点的度之间的关系
• 在同配网络（assortative network）中，高阶节点倾向于更多地连接到其他高阶节点，低阶节点也是如此
• 在异配网络（disassortative network）中，高阶节点倾向于更多地连接到低阶节点，反之亦然。

定义：

• k度节点的平均最近邻度函数：

  • 其中是从k度节点出到k'度节点入的概率

  • 如果没有相关性（中性网络-neutral network），有 pi：i度节点的比例

  友谊悖论指出，节点邻居的平均度通常高于其自身的度。这是由于在许多网络中： 即：一个节点更可能与中心（高阶节点）链接

• 度相关函数可以近似为：

  • 表示同配网络
  • 表示中性网络
  • 表示异配网络

图模型（随机图）

• ER模型：Erdos-Renyi models (ER)
• CL模型：Chung-Lu model (CL)
• 配置模型：Configuration model

ER模型

概念：

• G(n, m)模型：n个节点，m条边，任意选两个节点相连。——平均度：k = 2m/n
• G(n, p)模型：n个节点，任意两个节点之间以概率p相连（边数期望为Np）。——平均度期望：k = p(n − 1)
  • 令p = m/N，此时可以转化为第一种模型

边数分布：

• 为G(n，p)模型中有m条边的概率，令：（典型二项分布）

• 假设N很大而p（通常）很小，我们可以使用泊松分布（ 为平均边数的期望）近似二项分布：

度分布：

• 某个点度数为k的概率为：（ 为平均度的期望）

• 由于近似服从泊松分布，此类模型不生成hubs节点，即真实网络中常见的高阶节点。

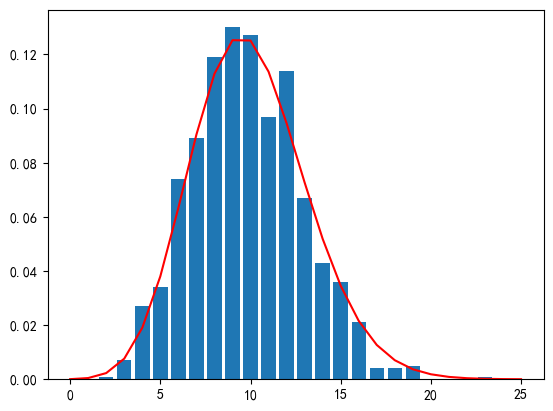
• 可以绘制度分布直方图，用poisson分布曲线可以很好地拟合

  

巨型连通分量（Giant connected component-巨片）：（期望平均度）——三种状态

1. ：亚临界状态；没有巨片，集群主要是树。

2. ：超临界状态；单个巨片，小集群主要是树。

3. ：连通状态；没有孤立的节点或小集群。

——从折线图可以看出，k为1是分界点，一旦超过1，巨片占比迅速扩大；到k = 7逐渐稳定达到100%

CL模型

伯努利Chung-Lu模型

模型：

• 网络G中的节点为：

• 每个节点的度为：

• 两个节点i和j连接边的概率为：（为图的体积——所有节点的度数和）

分布：

• 我们将定义为使用模型1获得的图G的分布： 其中图为获得的新随机图：

  • ，但一般情况下
  • 没有重复边
  • 有自环

——该模型在实际中不常用，其时间复杂度为

O(m) Chung-Lu模型

模型：

• 只需要的时间复杂度，更常用

• 在顶点V中选择条边，

• 根据多项式分布从V独立采样：

• 边可以重复，所以我们得到的是预期的边数而不是概率

分布：

• 我们将定义为使用模型2获得的图G的分布： 其中图为获得的新随机图：

  • 我们总是有
  • 允许存在多条边
  • 也允许有自环

注意：

• 对于模型II，我们可以忽略重复的多条边，这会减小图的总度期望（体积）
• 对于这两种模型，我们都可以忽略自边（自环），这会再次减小总体积

配置模型（Degree Sequence）

提出：

• Chung Lu模型是边生成的概率模型，生成度序列的期望和原来的相等。
• 对于配置模型，我们为节点指定一个精确的度序列
• 所有具有n个节点和这个精确度序列的图 被认为是以相同的概率出现的。

模型：

• 对于每个节点i，我们指定个残边（stubs）——半条边

• 残边随机互联

• 可能会产生自环或重复边

• 对于该模型，节点之间的预期边数为： 对于自环：

  边总数的期望为：

基准（小世界 幂律）

• 小世界网络
• 聚类系数
• 幂律网络
• Barabasi Albert和其他模型

小世界网络

背景：

• 真实图通常不像 ER图 或 CL图 具有均匀的度分布
• 真实图中的一些性质：
  1. 节点之间路径相对较短（小直径）(small diameter)
  2. 局部密度行为（三角形，社区）(triangles, communities)
  3. 大量的低度节点
  4. 存在高度节点（枢纽，权威）(hubs, authorities)

定义：如果特征路径长度（节点之间的平均距离）与节点数n的对数成正比增长，那么图就表现出小世界行为。

“六度分割”理论：今天的社会网络通常有较低的特征路径长度（任意两人之间的平均关系路径长度为6）

聚类系数

背景：

大多数网络，特别是社会网络，都表现出同质性（homophily）。——朋友之间分享好友的概率大于随机建立

衡量：

我们可以通过观察图中的三角形（图的传递性(graph transitivity)）或每个节点的邻居之间的边缘密度（聚类系数(clustering coefficient)）来衡量这一点。

定义一个图

1. 图传递性

   • 三元组（triad）是一个由3个节点组成的子图，形成一棵树；设为图G中三元组的数量。
   • 一个三角形（triangle）是一个有3个节点的完全连接的子图；设是图G中三角形的数量。

   图传递性定义为：

2. 聚类系数

   • 对于一个度数为的给定节点，让表示节点i的邻居之间的边数

   • 节点i的（本地）聚类系数定义为：

   • 它也被称为局部传递性，因为它对应于节点i的自我网络（ego-net）的

   图G的聚类系数定义为： 也被称为平均局部传递性

注意：和往往相似，但这其实是误导

• 考虑以下有n+2个节点（n个灰色节点）的图

  

  • ：，

  • ：红色节点，灰色节点

对于ER随机图来说，两个点之间形成边的概率为p，所以ER图的两个指标值都为概率p。

幂律网络

背景：

• 在幂律函数中，一个量按另一个量的幂进行变化

• 在度分布中很常见

• 设是度数为k的节点的比例 c是归一化常数

• 对于社会网络中的度分布，通常观测到的数值是

齐普夫定律：（Zipf’s law 二八定律是它的一个特例）

• 在书面语言中，从等级r=1开始，按出现的顺序递减排列词语

• 根据Zipf定律，等级为r的词出现的比例与1/r成正比

幂律函数是无标度或标度不变的：（scale-free / scale-invariant）

标度改变时，函数曲线的形状和函数的指数都没有变，即具有标度不变性

在复杂网络上任选一局部，由于其自相似性，局部网络的形态、规律、功能均与原网络不会发生变化，即在尺度伸缩时具有对称性。——类似于分型

• 定义的函数：

  • 其中只有常数作为乘数a的函数而变化

• 在实践中，我们可以从参数为γ的幂律分布中，在某个区间[dmin, dmax]内抽取一串度数。

• 然后我们通过配置模型或CL模型生成一个图

  • CL模型可能会出现孤立点：因为存在大量低（期望）度的节点

举例：

• 见notebook

总结：

• 幂律网络表现出的度分布为：

  1. 许多低度节点

  2. "长尾"（long tail）——高度节点的存在

     这样的高度节点被称为枢纽（有向图的枢纽和权威 hubs and authorities）

BA网络（Barabasi-Albert）

一种典型的幂律分布网络

概念：

• 这是一个优先依附模式的例子，也被称为富者愈富
• 逐个节点生成图：
  • 在步骤t=0时，从一些初始图（例如：空图，小集团-small clique）开始。
  • 在步骤t>0时，向现有的节点添加一个新的节点，其边数为（最多为）m
  • 新节点与（现有）节点i有一条边的概率与添加这个新节点之前节点i的度数成正比。
  • 继续下去，直到生成n个节点

性质：

• 该模型倾向于依附于高度节点，从而形成枢纽

• 同理，度数为k的节点的比例为：

• 存在几种变型

• ER随机网络就没有这种幂律分布特性