文章导航
菲尔兹数学科学研究所 复杂网络2019夏令营课程 学习笔记
社区结构
- 图划分（graph partitions）算法比较
- 图聚类算法
- 图上的集成聚类（ECG）
图社区
- 定义
- 谱分割
- Girvan-Newman聚类
- 基准：种植分区，LFR
- 模块度
- 算法
定义
两个基本假设：[Barabasi,Network Science]
- 一个网络的社区结构在其布局图中是唯一的。
- 一个社区是网络中的一个局部密集连接子图。
模型：
- 对于一个图
，考虑由一个节点 的子集诱导的连接子图C（C中的节点满足 ）。
内部外部度：
定义节点
的内部度（其在子图C内的度）： 节点i的外部度是：
其中
是节点i在G中的总度
强弱社区：
- 如果对每个节点
， ，则C是一个强社区（strong community） - 如果对每个节点
， ，则C是一个弱社区（weak community）
集团和核：
- 集团（clique）是G的一个完全连接的子图。
- k核（k-core）是G的一个最大连接子图，其中所有节点的度数至少为k
- 我们可以通过反复删除所有度数小于k的节点来找到k-cores
- 如果一个节点属于k-core但不属于(k+1)-core，那么这个节点的核心度（coreness）为k
簇（聚类）：
- 大小为k的图
的聚类（clustering）是一个节点 的分区，其中： - 所有
- 对于每个部分（或集群）
，其诱导子图 是连通的
- 所有
谱聚类
谱聚类（Spectral clustering）是一个庞大的话题，本课程只介绍明谱分割（spectral bisection）
参考：
https://blog.csdn.net/weixin_45591044/article/details/122747024
https://blog.csdn.net/SL_World/article/details/104423536
模型：
考虑未加权的无向图
，邻接矩阵为A D是节点度组成的对角矩阵
是G的（未归一化的）拉普拉斯系数矩阵 G中的社群结构与L的特征分解之间关系紧密
对于所有的
： 因此，当 时，使上述表达式最小化相当于使
求解：
讨论：
L是对称的和半正定的，所以所有的特征值都是实数和非负数。
L有最小的特征值0；这个特征值的倍数对应于G中连接组件的数量。
因此，我们可以对这些特征值进行排序，同时对它们各自的特征向量进行排序。
非连通图情况：
- 有至少两个0特征值
- 按照第二小特征值对应的特征向量，有0和非0两种情况，按这个分类即可。
连通图情况：
考虑一个连通图G。它只有一个0特征值。
在一个连通图中，特征向量
对应于费德勒向量中的 。 谱分割是基于费德勒向量（第二小的特征向量）中条目的符号。——正为一类，负为另一类
多个社区：
- 如果有2个以上的聚类，这样的过程可以被递归应用
- 这是一个分裂性层次聚类的例子
- 然而，它可能表现得很糟糕，可能会分割本来存在的社区
- 所以我们去
，再利用k-means等算法对得到的特征向量进行聚类
总结：
一般适用于分组数量已知的情况，核心是最小化割边总和并最大化每个簇的节点数
GN算法
Girvan-Newman算法
步骤：
- 计算每个
的边介数，并删除具有最高值的边 - 将生成的图按连通分支拆分（簇）并递归地应用该方法
- 这会产生一个聚类层次结构，我们可以将其表示为树状图
——根据一些标准选择最好的分区，比如模块度（modularity）、或指定集群数量
问题：
- 该算法的一个问题是它的时间复杂度：
- 对于非常稀疏的图，也有
，仍然很高 - 其他算法可以达到
或
基准
为什么要有社区基准模型？
- 测试和比较算法
- 控制噪音水平、社区规模等
- 真实图数据很少有真实值（ground-truth）
- 有ground-truth，但可能与基本假设不一致
种植-分区模型
Planted partitions model
- 固定节点数 n 和社区数 k，对于社区，我们：
平均分配节点到每个社区
或将每个节点独立分配给社区 i，概率为
，
- 对于分别在社区i和社区j中的节点对
，我们按照概率 添加边 - 可以指定
、
- 可以指定
LFR模型
Lancichinetti-Fortunato-Radicchi model
- 固定节点数 n
设定三个主要参数：
：节点度服从 的幂律分布；推荐值为 。 ：社区规模服从 的幂律分布；推荐值为 。 ：对于每个节点，这是连接到其他社区的边的预期比例，而 是其自己社区内的比例。
——
称为噪声水平或混合参数 - 把每个节点都分配到社区
- 存在允许重叠社区的变体
- 可以提供额外参数来限制度分布（平均和最大度）和社区大小（最小和最大）
- 从配置模型开始，重新连接节点以逼近目标分布
- 初始阶段可以使用BA等其他模型
基准代码生成 3 个文件：
- 包含节点标记为 1 的边列表的文件
- 包含节点列表及其社区成员的文件，社区也被标记为 1
- 具有度分布、社区大小分布和混合参数等统计信息的文件
讨论：
LFR 的可扩展性有些受限，一些可扩展的基准模型有：
RMAT ，生成具有幂律度数分布的图；在 Graph-500 中使用
BTER (Block Two-level ER)，生成服从幂律度分布以及社区结构的图
SBM（Stochastic Block Model），它也生成具有社区结构的图。
——它最简单的定义是种植分区模型的变体。
模块度
引言：
- Barabasi 的第三个基本假设：随机连线的网络缺乏固有的社区结构
- 模块度使用随机连接作为空模型来量化某些图分区的社区结构
模型：
考虑无向图
令
, , 为节点 i 的度数 设
当且仅当 ，否则为 0；设 当且仅当 当我们随机连线时，节点 i 和 j 之间的预期边数（概率）为：
令
，将图划分为 k 个簇。对于某些簇 ，定义： 展开为： 令： 代入可得：
模块度最终定义为：
我们将上面的第一项称为边缘贡献（edge contribution），将第二项称为度税（degree tax）
图的模块度
有时被定义为所有可能分区中上述指标所取的最大值
讨论（局限）：
Barabasi 的第四个基本假设：对于一个给定的网络，具有最大模块化的分区对应于最佳社区结构。
然而，模块化有一些已知的问题——"最佳 "可能并不总是转化为 "直观"。
基于模块化的算法受到分辨率限制问题的影响：
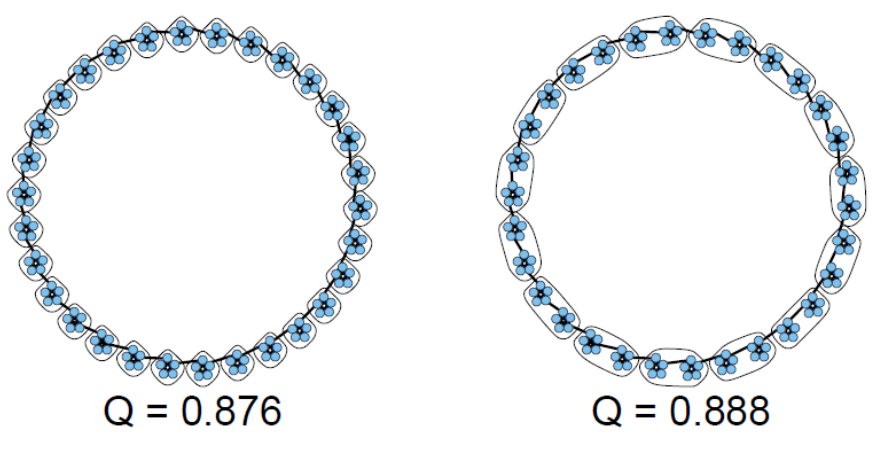
- 考虑l个大小为m的集团（m-clique）组成的环，
- 当
时，对相邻的集团进行分组，模块度高于每个集团自己形成集群 - 正如我们将说明的那样，一些基于模块化的算法因此倾向于对已有社区进行组合
- 考虑l个大小为m的集团（m-clique）组成的环，
算法
CNM：
CNM算法（Clauset、Newman、Moore），也称为快速贪心算法（Fast Greedy）
- 开始，每个顶点作为一个单独集群
- 选择最能提高模块度的一对集群（如果有的话），然后合并它们
- 当没有办法提高模块度的时候停止
- 复杂度：
，稀疏图更少
Louvain：
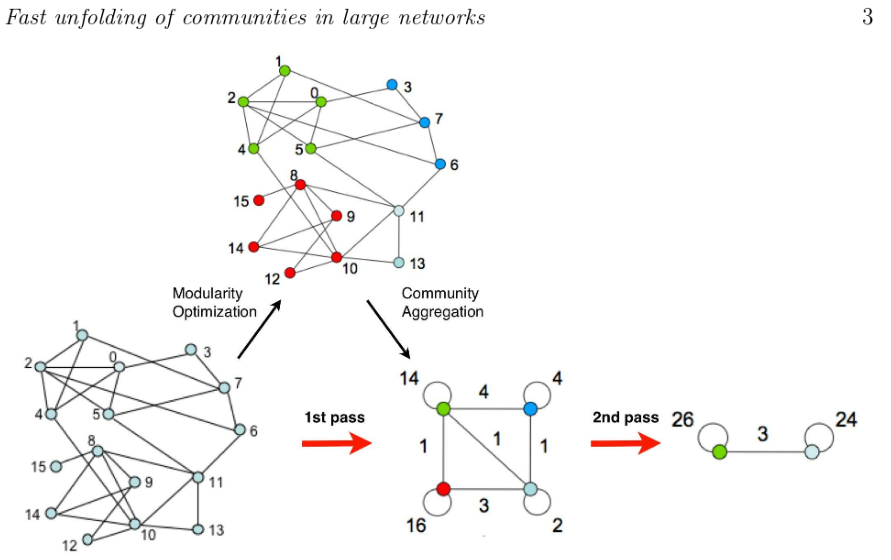
也称为多级算法（Multilevel algorithm）或快速折叠算法（fast unfolding）
- 开始，每个顶点作为一个单独集群
- 循环遍历每个顶点，将其移动到模块度增加最多（如果有的话）的邻居社区
- 重复以上步骤，直到没有任何提升空间为止
- 将每个社区折叠成一个节点并重新运行上述步骤——另一个层级
- 当图折叠到单个节点（或者当最后一级没有移动）时停止
- 复杂度：
Infomap：
- Infomap基于信息论：使用概率随机游走和压缩算法来实现
- 给定 G 和一个初始化分区方案，尽可能高效地编码随机游走
- 利用随机游走往往在同一社区中停留更长时间的性质
- 优化图方程：社区间游走的平均位数+社区内游走的平均位数
- 复杂度：
标签传播：
- 开始，每个顶点作为一个单独集群，有自己的簇标签
- 循环遍历每个顶点，每个顶点都采用其邻居中最流行的标签（使用随机来打破死锁）
- 当每个顶点具有与其邻域中最频繁出现的标签相同的簇标签时，算法停止
- 复杂度：
——注意：此算法速度很快，但并不总能收敛到一个解。
其他：
- WalkTrap：一种基于短距离随机游走的分层算法。它的复杂度是
。 - Leading eigenvector（前导特征向量）：基于模块化矩阵的谱分解。对于每个双分区，其复杂度为
Louvain和Infomap的算法目前被认为是最先进的。
2023年评论：应该是Leiden算法
图分区的比较（指标）
- 介绍：图聚类
- 常见的相似性测度量
- 与二元分类的联系
- 图感知度量 （Graph-aware measures）
- 拓扑学特征
图聚类
符号描述：
- A，邻接矩阵：
：顶点i的程度
术语解释：
- 图聚类/分割（clustering/partitioning）：将顶点分割成相连的子图
- 社区发现（Community finding）：并非所有的顶点都需要被分配到一个群组中去
- 模糊聚类（Fuzzy clustering）：节点不属于、属于一个或多个群组
图划分：
- 每个
诱导出一个连通子图 - 是连通分支的泛化
- 集群内的边密度大；集群间的边密度小
应用：
- 图聚类是关系型EDA（互联网数据分析）的一个重要工具
- 图尺寸缩减
- 社区检测
- 异常检测
- ……
- 如何挑选聚类算法？
- 集群的质量
- 稳定性
- 效率（时间空间）
- 其他：不需要指定聚类的数量（k）、集群的层次结构等
优化目标：
这是无监督学习，所以没有明确的目标函数
不同算法使用不同的目标函数：
- 模块度：
- N-cut
不同分割方法对比：
- 质量的衡量标准：
- 稳定性的衡量标准：同一算法的运行多次比较
- 比较算法之间的结果：
相似性
总体分类：
基于成对计数（Pairwise-counting）
基于信息论
基于卡方分布（
）
基于成对计数：
考虑对图节点的两个划分：
度量指标基于A和B里面各个集群中的成对元素
关键值为：
示例：
Jaccard 指数：
兰德指数
基于信息论：
基于 A 和 B 之间的互信息
关键值为：
示例：归一化互信息 (NMI)：
基于卡方分布：
关键值为：
示例：Cramer 的 V指标 和 Tschurprow 的 T指标
测量指标vs.大小分布：
问题：比较不同大小的分区时，这些度量指标表现怎么样？
实验（多次重复）：
：节点V的划分 ，V 的随机分区 ， - 测量
和所有分区 之间的相似性——期望所有相似度都很低
——结果：只有兰德系数变得接近1，其他都随着t的增大减小或趋向0
按概率进行调整：
实现 “在聚类结果随机产生的情况下，指标应该接近零”
成对计数指标的调整：
Jaccard 没有已知的调整形式
调整兰德指数定义为：
- 基于信息论和基于
的也可以针对机会进行调整 - 最常用的有：
- ARI：调整兰德系数
- AMI：调整互信息
——调整后的指标在随机下都趋近于0
二元划分
我们已经有了对比划分的指标，但我们根本没有考虑图拓扑。
测量相似性时应该考虑边吗？
这就引出了下面要讲的图感知测量，在这之前，要先讲下二元划分
边分类：
图分区可以由节点 V 上的集合分区表示
我们还可以考虑二元边分类（顶点是否在同一簇中）
——两端节点在同一簇的边 ——两端节点在不同簇的边 更正式地说，对于顶点分区 A，我们定义长度为 m 的二元向量
，其中，对于每条边 ： 更进一步地，可以利用此方法对类别1边子集的边进行搜寻。
二元分类器的评估：
考虑
和 ，两个二元边分类器。 用于比较二元分类器的四个基本计数是：
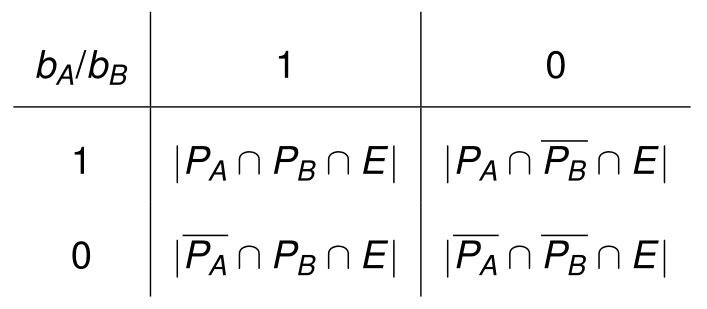
对应的各种度量指标如下：
图感知度量
（调整）图感知度量：
上一节的指标可以用二元分类向量的乘积表示：
我们提出一系列成对计数的图感知度量指标：（一个是普通、另一个是调整后的）
实验：
- 在LFR模型构建的社区中，调整图感知度量的性能指标都很好
- 不同种类的度量指标的度量效果不同（引子）
补充：
——图感知和图无关度量在解决问题方面具有相反的行为
图无关度量即前面说的普通相似性指标ARI等
- 设 G 的真实社区情况为 A， 并设 B1 和 B2 分别是 A 的粗化和细化
- 在某些情况下，在图无关度量下A更接近B2（细化）；在图感知度量下A更接近B1（粗化）
- 当使用图无关的度量时，集群的数量更多
- 图感知度量生成的集群的数量更少
- 这两种指标都获得高值是我们做图聚类所希望的
定理的公式化描述：
- 考虑Girvan 和 Newman 模型的变体 G(n, p, q, A)，用于研究具有社区结构的图族
- 图有 n 个顶点，A为分区结果
- p为随机选择两个节点，其中的边在同一分区内的比例；
- q为随机选择两个节点，其中的边在不同分区内的比例。
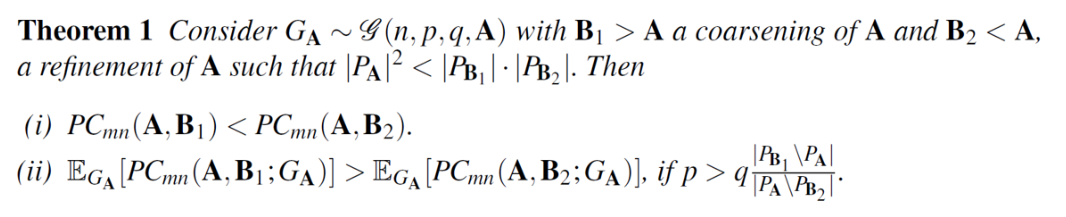
拓扑特征
验证集群的另一种方法是比较集群的拓扑特征：参考Orman et al.,arXiv:1206.4987
示例：对于具有
个节点和 个边的社区 —— 缩放密度(scaled density)：
内部传递性(internal transitivity)：
其中
是 c 中 i 的邻居之间的边数， 是 c 中 i 的度数。
可以将特征作为簇大小的函数进行比较——比较聚类算法结果和ground truth的图形相似度
结论
- 使用调整后的基于集合的相似性度量，可以减少度量对分区粒度的偏差，消除随机性
- 图无关（ARI，AMI）和图感知（AGRI）度量是互补的：在评估算法的优越性时应同时使用它们
图的集成聚类（ECG）
- 共识聚类和 ECG
- 分辨率和稳定性
- LFR 图上的研究
- 一些真实的图示例
- ECG 权重
- 在异常检测中的应用
ECG
符号说明：
- 令图 G = (V , E), V = {1, 2, . . . , n}, 为无向图
- 对于每个 e ∈ E，边可以具有权重 w(e) > 0，或者考虑所有 w(e) = 1
- 令
是大小为 的 V 的一个分区 - 定义指示函数
，表示
图聚类的目标：好的、可扩展的、通用的——注意这是无监督学习
- 关联强度的度量
- 聚类的层次结构
- 不需要或尽量少调整参数
——使用集成学习（Ensemble learning）来实现这些目标：利用生成的多个分区来集成——如何合并多个图分区？
ECG算法：
ECG算法是图的共识聚类算法。步骤是：
- 生成步骤：来自 Louvain (ML) 算法的 k 个随机的 1级别（level-1） 分区：
。 - 集成步骤：在初始图 G = (V, E) 的重新加权版本上运行 ML。 ECG权重是通过联合获得的。
边
是人工定义的最小权重 表示是否在 的簇中共现。
通过示例可以看到，一个社区内的节点间的边在集成后权重变大，集团（clique）内的边尤其明显，而社区间的边集成后权重减小，变得很容易区分
分辨率和稳定性
分辨率：
- 基于模块化的算法存在分辨率限制问题：举例集团组成的环，相邻两个组合后模块度更大
- w* 值较小的 ECG 算法缓解了这个问题
- 使用 level-1的Louvain 作为弱学习器是关键——第一层louvain不会聚合那些环上的边
实验：
- 在广义集团环上ECG算法表现也很好：将ECG和louvain、InfoMap比较，分别考察环上连接集团边数从1增加到5时的表现
- 即使噪音很大，权重仍然很显著：当噪声很大时，同一集团中的边权重仍然显著
- 在LFR生成的社区发现上，ECG算法能够很好地保留原始数量：level1的louvain数量过多，最终的louvain数量过少
- 在上一章的图感知与图无关度量上表现也很好
稳定性：
- Louvain 和其他算法的已知问题：多次重新运行同一个算法会得到不同的结果
- 我们通过运行每个算法两次并应用一些比较措施（例如 ARI）来量化稳定性
实验：
- ECG相比louvain在稳定性方面有了很大的改善
- 实证研究表明，结果对参数的选择不是很敏感（低级聚类次数k和最小权重W*）——不过一般情况下k越大、W*越小效果越好。
LFR 图上的比较研究
- 论文在数千个 LFR 图上比较 8 种算法
- 各种指标水平都是ECG较好
- 本研究只考虑γ1 = 2, γ2 = 1，在不同参数的LFR模型下，ECG大部分情况下都比较好
一些观察结论：
- InfoMap 在大小相同的小型社区上提供最佳结果
- ECG 在其他情况下提供最佳结果
- ECG 的效果始终优于单个 Louvain (ML)
真实网络
- 足球俱乐部网络
- ECG和InfoMap都取得了最佳结果
- YouTube网络
- 1,134,890 个节点（用户）和 2,987,624 条边（好友关系）
- 2-core 仅覆盖 41.1% 的顶点
- 8,385 个社区被声明为用户组，这些社区从拓扑角度来看非常薄弱
- 只有 12 个合格作为弱社区，外部度与总度的比率低于 0.5 我们将此比率扩展到 0.75（类似于 LFR 图中的 µ）
- 在图感知度量上ECG比InfoMap略胜一筹
权重
ECG 重新加权有助于提升聚类准确性和稳定性
我们讨论了计算的 ECG 权重的其他一些应用
- 我们定义了一个新的社区强度指数 (CSI)
- 我们展示了如何使用权重来放大种子顶点
社区强度指数CSI：
- 边界（0 和 1）附近的 ECG 权重的双峰分布(bi-modal distribution)表明了强大的社区结构
- 我们提出了一个基于点质量 Wasserstein 距离（推土机距离（Earth Mover's distance））的简单社区强度指标 (CSI)
定义：
- 对于所有边
，以及来自 ECG 的 ，我们定义： 使得
关联强度：
- 从图上直观看出高 ECG 权重表示强关联
- 从经验上比较 ECG 权重和三角形出现次数：正相关关系
我们可以使用 ECG 权重作为自我网络的替代方案来放大种子节点
给定一个种子节点 v：
- 确定它所属的集群
- 删除所有 ECG 权重低于某个阈值 τ 的边
- 放大包含 v 的连通分量
- 增加 τ 可以对其进一步放大
——使用此方法可以很好地保留ground truth里面的真实同社区节点
异常检测
最近提出了CADA（community-aware anomaly detection社团感知异常检测）
CADA：
对于每个节点
：v 的邻居数。 ： v 属于出现次数最多社区的邻居数（通过图聚类）。
——
实验：
