【复杂网络】高级操作

文章导航

× 文章目录

1. 1. 图嵌入
   1. 1.1. 概述
      1. 1.1.1. 算法
   2. 1.2. 比较框架
      1. 1.2.1. 概述
      2. 1.2.2. 几何Chung-Lu(GCL) 模型
      3. 1.2.3. 解GCL模型
      4. 1.2.4. 分歧分数算法
   3. 1.3. 示例
2. 2. 关系数据上的半监督学习
   1. 2.1. 简介（转导学习）
      1. 2.1.1. 应用-示例
   2. 2.2. 无向图
   3. 2.3. 其他图
      1. 2.3.1. 有向图
      2. 2.3.2. 枢纽/权威型网络
      3. 2.3.3. 混合图
   4. 2.4. 超图
      1. 2.4.1. 模型
      2. 2.4.2. 分类数据（应用）
3. 3. 超图模块度和聚类
   1. 3.1. 普通图聚类（回顾）
   2. 3.2. 超图模块度
      1. 3.2.1. 超图表示
      2. 3.2.2. 超图Chung-Lu模型
      3. 3.2.3. 超图模块度
   3. 3.3. 超图聚类
      1. 3.3.1. 概述
      2. 3.3.2. 示例
      3. 3.3.3. 证明
      4. 3.3.4. 算法
      5. 3.3.5. 实验

菲尔兹数学科学研究所 复杂网络2019夏令营课程 学习笔记

高级操作

• 图嵌入（Graph Embedding）
• 图半监督学习（SSL）
• 超图

图嵌入

Graph Embedding，也叫图表示学习(Network Representation Learning)

1. 图嵌入的快速概述
2. 一些算法：node2vec、LINE、Verse
3. 比较嵌入算法的框架
4. 示例

概述

目标：

• 将网络（节点）映射到向量（特征）空间

• 将相似节点映射到向量空间中的附近位置。“相似”可能有不同含义：
  • 图拓扑上较近
  • 图中相似的角色（例如：度相似）
  • 相似的节点属性

应用实例：

1. 特征学习（不是特征工程）
2. 可视化
3. 链接预测
4. 社区检测
5. 异常检测
6. 网络演化（动力学）

形式化描述：

• 输入：G = (V , E)
• 输出：特征向量

算法

——大部分算法基于随机游走和 用于词嵌入的 SkipGram 方法

• 词的语义由其上下文决定(A word can be characterized by the company it keeps)
• 相似上下文中的词（相近的词）具有相似的含义
• 考虑每个单词周围的窗口；构建“词向量”（例如：word2vec）
• 使用这些作为训练数据

SkipGram：

使用滑动窗口邻域对每个词上下文的相关词进行组合，构建“词向量”

DeepWalk（深度游走）：

• 单词——对应于节点
• 句子——对应于图 G 上的随机游走
• 句子中的词频呈现幂律分布——游走中的顶点也呈现幂律分布

node2vec：

• 定义了有偏随机游走（biased random walks）混合了广度和深度优先搜索
• 关键参数：
  • p：控制重新访问同一节点的概率（留在附近）
  • q：控制探索更远的概率

概率选择

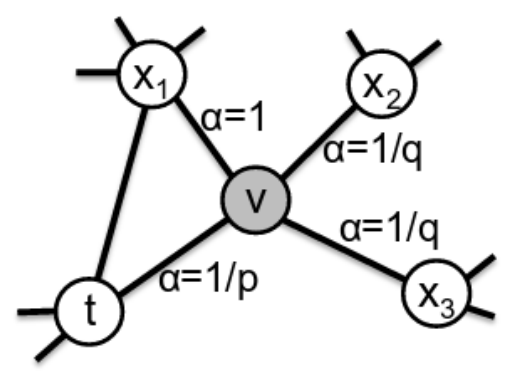
• 参数允许在以下之间进行权衡：
  • 低 p：在本地探索；这将侧重于图形拓扑结构中的社区结构（同质性）；
  • 低q：探索更远；这允许捕获节点之间的一些结构相似性（例如：集线器hubs，网桥bridges）；

其他算法：

统计表见课件

在我们的测试中使用了：

1. node2vec：q=1，p各不相同
2. VERSE：来自相似性度量（具有个性化page rank）的多功能图嵌入算法：使用默认参数
3. LINE：Large-scale Information Network Embedding（大规模信息网络嵌入），它使用邻接矩阵的近似分解来尝试保留一阶和二阶邻近度

比较框架

• 我应该使用哪种嵌入算法？
• 如何选择参数？
• 我怎么知道这种嵌入算法对图的表示就好？
• GIGO：向量空间中的错误表示会导致错误的结果......

算法之间的结果可能会有很大差异，并且随着参数的选择也会有很大不同

核心：使用嵌入后的向量构建同分布随机图，比较随机图和原图的JS散度，若很小，说明相近，进而说明嵌入效果良好

概述

框架模型：

给定具有度分布 的 n 个顶点上图 G = (V , E) 及其顶点到 k 维空间的嵌入，。

• 我们的目标是为这个嵌入分配一个“分歧分数”(divergence score)。
• 分数越低，嵌入越好。这将使我们能够在不同的维度上比较多个嵌入的结果

总述：

• 非随机图表现出类似社区的结构，所以我们一般：
  1. 将节点分组为集群
  2. 测量簇之间和簇内的边缘密度
  3. 通过 计算散度分数 将其与嵌入（矢量）空间中空间模型的预测密度进行比较
  4. 选择得分最高的嵌入
• 我们的框架中有两个主要部分：
  1. 图拓扑视图：一个好的、稳定的图聚类算法；我们默认使用 ECG，但我们也尝试使用 Louvain 和 InfoMap
  2. 空间视图：我们引入了基于度分布 w 和嵌入 ε 的几何 Chung-Lu (GCL) 模型。

几何Chung-Lu(GCL) 模型

Chung-Lu 模型：（引子）

• 在原始的 Chung-Lu 模型中，每个集合 被独立采样为边，概率为：

• 它产生的分布保留了每个顶点的预期度数

几何Chung-Lu(GCL) 模型：

• 考虑预期的度分布：

• 以及节点 的嵌入，以便我们知道所有距离：

• 模型应该满足 ，g为递减函数，因此长边的出现频率应该低于短边

• 我们使用以下归一化函数 其中 是一个定值： ——我们使用裁剪（clipping）来强制 和/或
  • 当 α = 0 时，此模型退化为原始的 Chung-Lu 模型，忽略了节点对的距离
  • 参数 α 越大，对长边的厌恶越大
  • 因此，模型的唯一参数是 α ∈ [0, ∞)
  • 在实践中，我们会尝试一系列值并保持最佳拟合。

• GCL模型是基于顶点集 上的随机图 其中 vi, vj, 形成一条边的概率为：

  • 权重选择：

• 顶点vi的度期望为：

定理：当 G 中的最大度数小于所有其他顶点的度数之和时，仅有唯一的权重选择。

——由于 G 的每个连通分量都可以独立嵌入，我们可以假设 G 是连通的，因此 G 的最小度数至少为 1。因此，除非 G 是 n 个顶点上的星形，否则这个非常温和的条件是平凡的。

我们要做的，就是通过选择权重，使得度分布期望等于原图度分布。

解GCL模型

我们使用一个简单的数值近似程序

1. 从任意向量开始

2. 给定 ，如果我们以如下概率在 vi 和 vj 之间引入一条边：

3. 那么 vi 的度期望将是：（这对应于上小节度期望）

4. 通过用 替换 来调整权重，使 与 匹配
   • 这也会影响 的其他值，并且 其他部分的变化也会影响 自身。
   • 因此，我们让每个顶点向正确的方向迈出一小步
   • 这个过程很快收敛到理想状态：对于所有 i， 都非常接近 。

5. 迭代步骤：

   • 对于每个 i，1 ≤ i ≤ n，我们定义

   • 重复调整过程直到

   • 定义 ε = 0.1 、 δ = 0.001

分歧分数算法

计算嵌入分歧分数（embedding divergence score）的算法

给定 G = (V, E)，它在 V 上的度分布 w，以及它的顶点的嵌入，我们将执行接下来详述的五个步骤

• 通过算法，我们获得 ，嵌入的分歧分数
• 我们可以应用这个算法来比较几个嵌入算法的分歧分数指标，选出最好的（最小的）那个

第一步：

在 G 上运行一些稳定的图聚类算法以获得顶点集 V 的分区 ，一共产生 个社区 。

此教程中使用ECG，其实任何稳定的算法都可以。

第二步：

令：

• ：两个端点都在 中的边的比例
• ：一个端点在 中且另一个端点在 中的边的比例

定义： ——这些向量从 图 G 的角度表征分区 C，嵌入 不影响 和

---

——接下来我们在 α 的一系列值上重复步骤 3-4

第三步：

给定 ，使用的GCL 模型。

从这个模型，我们计算：

• ： 内边的比例期望
• ： 中一个端点和 中另一个端点的边的比例期望

定义： ——这些向量从 嵌入 的角度表征分区 C

第四步：

计算 和 之间的距离，以及 和 之间的距离

我们使用 Jensen-Shannon 散度 (JSD)： ——这是给定 α 的（分歧）分数。

第五步：

从重复的步骤 3-4，我们获得了一系列

选择

将分歧分数定义为： 总结：

• 为了比较同一个图 G 的多个嵌入，我们重复上面的步骤 3-5 并比较分歧分数（分数越低越好）。
• 步骤 1-2 只执行一次，因此我们对每个嵌入使用相同的图划分算法到 个社区

示例

• 空手道俱乐部：找到最适合嵌入的α值
• 足球比赛：使用分歧分数选择最合适的嵌入算法
• LFR 数据集：使用此方法选出的最好和最坏embedding算法效果

关系数据上的半监督学习

简介（转导学习）

我们使用一种转导学习（transductive learning）的方法:

• 没有显式地构造任何模型
• 学习是“基于数据”的
• 在图上使用正则化框架，正则化包含以下两种情况：
  1. 局部结构：与稀缺标记顶点一致
  2. 全局结构：所有顶点的平滑

形式化描述：

设，

设函数 ，同时定义两个函数的内积：

• 我们定义一个函数 满足：

  • 是一个依赖于G的泛函：平滑泛函

    ——取决于图的类型：无向、有向、联合链接(两者都有)

  • 编码先验知识(顶点标签)

    ——取决于要解决的问题：

    1. 二进制分类：
    2. 排序：
    3. 无监督：

  • :平滑度(smoothness)和一致性(consistency)之间的权衡

应用-示例

• 给出一个包含一些“有趣”实体的大型图
• 求解以放大附近的顶点

最终可以：

1. 获得未知实体的排名
2. 能可视化关键子图
3. 网络安全环境中的几个应用
   • 异常检测
   • 恶意软件检测
4. 图和超图通常太大，不适合直接分析或可视化

无向图

图模型：

• 设无向图为 是所有 的边权 的矩阵。
• 设D为节点度的对角线矩阵：

无监督N-cut问题：（回顾）

• 对于一个分割 其中： 这可以被视为具有转移概率 的随机游走：

• 这个问题可以通过松弛实值来解决 其中 且： 是(归一化)图拉普拉斯矩阵

——这被称为归一化谱聚类（normalized spectral clustering）

半监督问题：

概述：

• 拉普拉斯矩阵也出现在半监督问题中：

• 如果节点接近(很大)，那么它们应该有相似的标签()，以保持较小
• 在整个图上，这相当于保持较小

• 这可以看作是找到一个“平滑”函数f，它在图的密集区域中变化很小，但在稀疏区域中变化更大。

形式化描述：

• 现在假设顶点上有一些初始(种子)值y：

• 将半监督问题定义为关于图拓扑的“平滑性”和关于y的一致性之间的权衡，例如: 令 , 则有： 若 , 且 ,存在一个封闭式解： 其中:

  , 归一化图拉普拉斯矩阵

  , 平滑矩阵

求解：

可通过多种方式获得：

1. 迭代方法:

   • 从开始，

   • 迭代

2. 它可以写成一个 对角占优 的线性问题，其反演技术存在，且复杂度为，其中m为非零项的个数
3. 通过共轭梯度法

4. map-reduce框架具有良好的可伸缩性

其他图

有向图

形式化描述：

• 定义进出节点度： .

• 上的然随机游走的转换概率为：

• 设 为唯一平稳分布，即： 这需要定义一个传送随机游走（teleporting random walk）——用于描述随机游走的概率

• 考虑泛函：

• 正则化问题和之前一样 其中 是转移概率的矩阵， 平稳概率的对角矩阵。（和无向图的差别在平滑矩阵S上）

• 和之前一样: .

——这是对无向情况的推广。对于无向图，随机游走的概率是固定的： ——此时平滑矩阵退化为无向图情况：

枢纽/权威型网络

Hubs&Authorities graphs

概述：

考虑顶点的两种可能角色:

• 具有高“入度”的权威(authority)
• 具有高“出度”的枢纽(hub)

对于有向图， u是“枢纽”，v是“权威”

平滑矩阵：

1. 权威型：

   定义节点 和 相对于节点 的权威距离为： 由此我们建立了平滑矩阵：

2. 枢纽型

   我们同样定义相对于节点 的枢纽距离为： 平滑矩阵：

求解模型：

令 ，其中 , 我们可以得到： 对于枢纽型我们可以类似地得到 . 令： 我们可以像以前一样解决正则化问题：（带入平滑矩阵求解即可） 对于一个无向图： .

混合图

我们可以将平滑泛函推广为 其中 基于随机游走， 是“枢纽&权威”平滑

这允许3种衡量顶点“接近”的方式：

1. 存在一条短路径
2. 指向几个公共顶点
3. 由几个公共顶点指向

——2和3对于无向图是一样的

超图

模型

符号说明：

对于(无向)超图，定义:

• ：超边集合——超边为节点子集
• ：超边权值
• ：节点度
• ：“超边度”
• 关联矩阵
• 权重矩阵，
• 节点度矩阵，
• 超边度矩阵。

Ncut问题可以推广到超图：

1. 超图体积

   对于一个分割 ，令： ——对于最后一个表达式，如果e被映射到分割的两端，分子是将被切割的“边”的数量。（就是转为普通图以后的割边数）

   可以再次通过随机游走来说明: 通过定义节点转移的平稳分布 得到以下结果：

2. 超图拉普拉斯矩阵

   解松弛后的问题得到与用图相同的形式，但是有 当所有 时，有: 也就是拉普拉斯矩阵的一半，因此可以定义为超图拉普拉斯矩阵

3. 问题定义

   我们定义了与图相同的半监督问题: 其中: 以上问题的解又下式给出：

4. 随机游走模型1

   • 从顶点u，随机选取 的超边e
   • 随机选取一个顶点 ，然后跳转到v

   我们可以将上面的超图视为一个加权邻接矩阵为 的普通图，其中： 行和为：

   • 如果所有 , 我们有

   • 而对于 我们有 , 所以

   其中A是这个超图的图表示的(加权)邻接矩阵

   因此，对于此随机游走模型，将G视为图和将G视作超图，转导学习问题的解将有所不同

   ——需要进一步改进

5. 随机游走模型2（改进）

   我们定义一个新的随机游走如下:

   • 从顶点u，随机选取 的超边e
   • 随机选取一个顶点, ，然后跳转到v

   我们可以将上面的图视为一个加权邻接矩阵为 的普通图，其中： 行和为： 邻接矩阵表达式为:

   其中 是对角阵，其元素为： .

   在这种情况下，调整后的超图Laplacian矩阵采用以下形式:

   • 如果所有，我们得到，其中A是这个超图的 图表示 的(加权)邻接矩阵

6. 有向超图的情况

   我们可以推广到有向超图，其中: 表示每个超边缘的尾部(tail)和头部(head)

   向多个收件人发送电子邮件是有向超边的一个例子

分类数据（应用）

超图可以用来对分类数据建模

• 示例：“蘑菇数据集”(UCI ML存储库):
  • 22个分类属性，23个物种的8124个观察值
  • 目标：二分类——可食用或可能不可食用
  • 每个分类属性建模为一个超边
    • “帽形=钟形”
    • “帽形=圆锥形”

学生作业：

• 用Python编写超图转导学习代码
• 在分类数据上验证已发表的结果——与图模型进行比较
• 研究权衡参数α的影响
• 提出并探索顶点嵌入框架

说明：

• 转导学习
  • 颜色代表蘑菇的分类：能不能吃
  • 参数α对结果值的量级有较大影响
  • 排序结果基本相同
• 嵌入
  • 顶点嵌入是一个热门话题
  • 尝试从不同初始值运行TL（转导学习）过程
  • 生成多维顶点表示
  • 和随机游走类似

超图模块度和聚类

1. 普通图聚类：模块度和Chung-Lu模型
2. 超图的模块度
   • 超图Chung-Lu模型
   • 严格超图模块度
   • 其他超图模块度
3. 超图聚类

普通图聚类（回顾）

模块度：

我们可以把图G的划分 的模块度写成: 叫做边贡献（edge contribution）——社区内的边相连的数量

叫做度税（degree tax）——社区节点相关的边在随机图的数量

Chung-Lu模型：

• 只需要的时间复杂度，更常用

• 在顶点V中选择条边，

• 根据多项式分布从V独立采样：

• 边可以重复，所以我们得到的是预期的边数而不是概率

• 我们将定义为使用模型2获得的图的分布：

  其中图为获得的新随机图：

  • 新图的度期望为：

  • 我们总是有

  • 允许存在多条边

  • 也允许有自环

——引理：图G的模块度函数中的 度税 是图 上 边贡献 的期望值。

我们能把这个模型推广到超图吗?

超图模块度

超图表示

背景：

• 存在比图更复杂的关联关系——涉及多个实体
• 传统图经常以两两之间的关系表示——丢失信息

超图：

• 超图 其中，
• 超边 其中，
• 边可以有权重
• 我们考虑无向超图

超图

——有些数据更适合用超图建模：电子邮件交换、跟踪主机代管、分类数据建模、数值线性代数

然而在实际操作中：

• 数据科学中，很少有基于超图的算法
• 它们通常比较慢
• 有些有等效的普通图表示

——问题：我们能在超图上定义模块度函数吗？

超图Chung-Lu模型

符号说明：

考虑一个超图 其中节点为： .、

超边 是节点数大于1的节点集合 的子集: 中顶点 的多重性（权值）

是超边 的大小

, 是节点的度

是节点集合的体积

生成概率：

设 是大小为 的节点集的集合，即： 随机模型中的超图是通过独立随机实验生成的。 对于每个 使 ， 产生 的概率为： 其中 .

度期望： ——我们使用Chung-Lu模型的这种泛化（超图Chung-Lu）作为零模型(度税)来定义超图模块度

超图模块度

设， ，是V的一个分区方案。对于尺寸大于2的边，可以使用几个定义来量化给定A的边贡献，例如:

1. 一条边的所有顶点都必须属于其中一个社区——这是一个严格的定义
2. 一条边的大多数顶点属于其中的一个社区
3. 一条边的至少2个顶点属于同一社区——当我们用超图的2段图表示代替超图时，隐式地使用了这种方法

严格超图模块度：

的边贡献为： 在 上的严格模块度定义为标准模块度的自然延伸，如下所示： 也可以写成： 和超图Chung-Lu模型的关系：

我们将Chung-Lu模型II推广到超图上：

• 对于每个d，选取 个边 ，其中每个 独立地从V中采样，且

• 我们将定义为使用上述模型获得的超图的分布：

  其中超图为获得的新随机图：

  • 新超图的度期望为：

  • 我们总是有

  • 允许存在多条边

  • 在一条边内可以有重复的顶点

——引理：超图 的模块度函数中的 度税 是超图 上 边贡献 的期望值。

其他超图模块度：

• 我们可以根据边贡献的许多自然定义来调整度税，例如多数定义

  在这种情况下 改成了只要大于边内节点数的一半即可

  ——这相当于 变成了

  超图划分的多数模块度函数为：

• 将H分解为d-uniform 超图，得到如下的度无关模块度函数： 这和以前一样，但是对于每个的d，将通过计算的体积替换为通过计算的体积

  最后，我们可以推广模块化函数，以允许加权超边

超图聚类

概述

我们在超图上寻求一个划分 , 使严格超图模块度 最大化.

集合 对于节点集 的所有划分来说是巨大的.

令 并定义： 这个函数将 的一个子超图映射到其连通分量在 上划分的函数.

我们定义一个等价关系： 并定义一个商集 .

商集（quotient set）是集合论的基本概念之一，指由集合和该集合上的等价关系导出的集合。设～是非空集合A的一个等价关系，若把以A关于～的全部等价类作为元素组成一个新的集合B，则把集合B叫做A关于～的商集合，简称为商集，记作B=A/～.

定义规范表示映射： 它将等价类映射到类中最大的成员: .

设 是 在正则表达式 上的像（也就是输入 输出的值域区间）.

我们将证明最优解在 中，它是一个子集，规模最大为 .

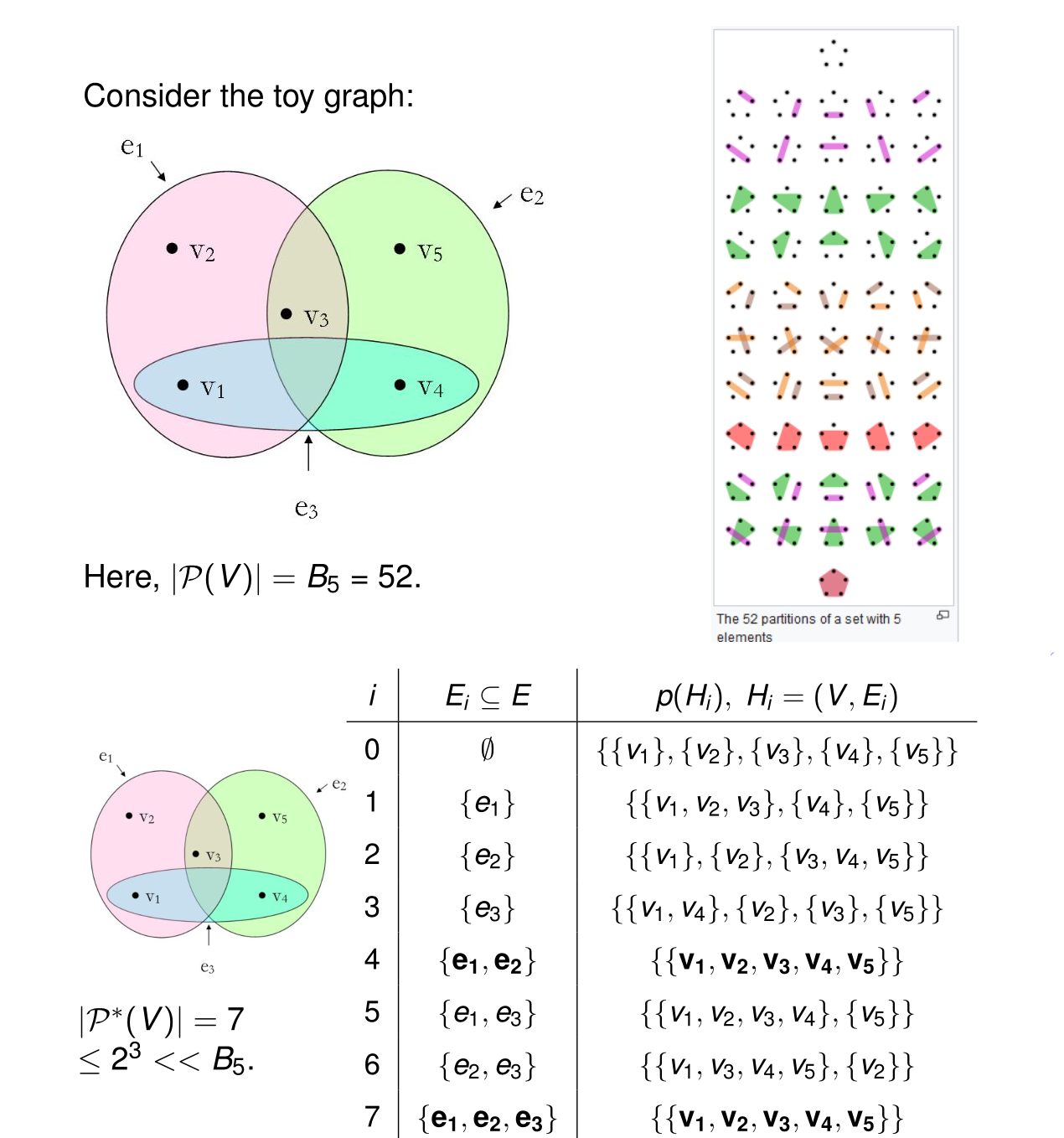
示例

上述5节点的超图，对其进行划分， 共有B5 = 52种可能

而 只有7种，远小于52中——缩小了搜索范围

证明

引理1：设 为超图， 是 的分区. 如果存在 使得 , 则 的边贡献为 , 其中 是 的典型代表 的边集。——即部分子集超边的比例。

引理2：设 是一个超图， 是 的任意划分。如果 是 的细化， 的度税小于等于 的度税，当且仅当 时取等号。

——我们证明了对任意分区，存在某个 使得 是该分区的一个细化，且具有相同的边贡献。

定理：设 为超图， 如果 使模块度函数 最大化，则

算法

前面的结果给出了定义启发式算法的步骤:

1. 循环遍历 ，令

2. 找到 并计算 的边贡献

3. 找到 并计算 的度税

在 中寻找合适组合的简单方法:

• 贪婪随机: 把超边随机重新排列，当 增加时，将其按顺序添加到 ; 重复这一操作;
• 类CNM: 在每一步中寻找添加到 的最佳边。

Hypergraph-CNM算法：

数据输入: 超图
结果输出: , 针对模块度函数 对 的一个划分
初始化 ： 每个节点独自为一个社区，计算对应的模块度 ;
repeat
foreach do
设置
end
foreach 接触到 中两个或更多的部分 do
计算新分区 ：将原始 中被 接触到的分区合并得到的分区;
计算新分区对应的模块度函数 ;
end
选择具有最大模块度函数值 的 ;
if then
， ;
end
until ;
输出: 和

实验

——好用吗？得到的模块度是最大模块度吗？

小demo：

• 建立超图，有3个社区，20个顶点，50条边，大小为2≤d≤5
• 添加3≤k≤60条相同大小的随机边
• 在k值范围内多次运行随机算法(重复25次)
• 对于每个k，计算平均调整兰德指数;

——结果：随着添加随机边的增加，聚类结果逐渐变差，但在随机边数小于30时，聚类效果还是OK的

合成超图：

• 在不同坡度的平面上沿3条线生成噪声点
• 添加一些随机点
• 选择3或4个点的集合(超边)
  • 都来自同一条线(“信号”)
  • 不来自同一条线(“噪声”)
• 采样超边，其中点对齐良好，因此预期的信号与噪声的比例为2:1

我们考虑3种不同的情况：(i)主要是3-边，(ii)主要是4-边，(iii)在3和4-边之间平衡。

在(加权)普通图上通过鲁汶聚类顶点。——我们观察到相比于普通图模块度，Hcut（不相交超边的数量）和超图模块度相关性更高

DBLP超图：

——引文网络

• 小型合著者超图，有1637个节点和865个大小为2到7的超边。
• 我们比较了鲁汶(超过2-section)和超图-cnm(严格模块化)两种算法

——与Louvain算法相比，基于超图模块度 的算法倾向于切割更少的大边，代价是切割更多的2节点边

---

总结：

已有工作：

• 超图的广义Chung-Lu模型
• 超图的广义模块度函数
• 超图聚类算法的步骤
• 两种简单的启发式算法：贪婪随机和超图CNM

未来工作：

• 更直观地理解模块化函数
• 更好的、可伸缩的聚类算法
• 真实数据集实验