文章导航
研一上系统优化大作业，解决实际问题。
——LR Algorithm Based on Interleaved Subgradient Method and Its Application in Multistage HFSP
Abstract
In order to reduce the complexity of the solution and shorten the calculation time, an improved Lagrangian relaxation algorithm combined with the interleaved subgradient method is proposed for the problem of the total weighted completion time of the multi-stage mixed flow shop. An integer programming mathematical model that comprehensively considers the finite waiting time and workpiece release time is established. An interleaved subgradient method is embedded into the Lagrangian relaxation algorithm, so that a reasonable interleaved subgradient direction can be obtained by approximately solving the Lagrangian relaxation problem. Search in this direction, gradually reducing the distance to the optimum point. The effectiveness of the proposed algorithm is verified by simulation experiments. Comparing the proposed algorithm with the traditional Lagrangian relaxation algorithm based on the subgradient method, the results show that the proposed algorithm can obtain better near-optimal performance in a shorter computing time in terms of the solution quality and computation efficiency , especially for large-scale problems.
Key words: systems engineering; interleaved subgradient method; Lagrangian relaxation; multi-stage hybrid flowshop problem; total weighted completion time.
Background and motivations
The Hybrid Flow Shop Problem (HFSP) can generally be described as: A set of workpieces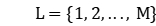 
is processed through 
processing stages in the same processing sequence, and each stage 
is composed of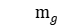 
isomorphic parallel machines, at least one processing stage with 
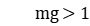; each workpiece is processed on at most one isomorphic machine in each stage; each machine can process at most one workpiece at any time, and each workpiece can only be processed on one machine at any time. Therefore, the problem to be solved by HFSP is to assign the workpieces to the machines and determine the scheduling of the workpieces on the machines at each processing stage, while also optimizing a given objective function[1,2].
This paper studies a kind of more complex HFSP, which is different from the general HFSP:
· Workpiece 
has a waiting time limit between two adjacent processing stages;
· Each workpiece can only be used for processing at time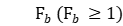 
;
· Transport time between adjacent processing stages is not negligible.
Gupta proved that the two-stage HFSP is NP-hard, even though there is only one machine for one processing stage. Therefore, the more complex HFSP studied in this paper is also NP-hard[3], which makes it particularly important to explore approximate algorithms for solving such problems.
As an optimization-based approximation algorithm, the Lagrangian relaxation (LR) algorithm has the basic idea of decomposition and coordination. For the actual scheduling problem, through a reasonable design, the algorithm can obtain nearly optimal solution with quantifiable quality in a reasonable computing time[4]. The traditional LR algorithm relaxes the machine capability constraint by introducing the Lagrange multiplier vector, and then decomposes the formed relaxation problem into multiple workpiece-level sub-problems, uses dynamic programming to optimally solve these sub-problems, and then uses the sub-gradient method to update the multiplier. sub-problem, using heuristics to convert the solution of the sub-problem to a feasible solution to the original problem. The above process is repeated until certain stopping conditions are met.
However, when the scale of the actual problem is large, the computational complexity of optimally solving the Lagrangian problem by dynamic programming also increases, which makes the solution quite time-consuming. Therefore, this paper introduces the interleaved subgradient method in the LR algorithm, which is a special case of the surrogate subgradient method[5], which requires each iteration to optimally solve a Lagrangian problem and saves the calculation time. The purpose is to obtain better solutions to large-scale problems in a shorter computational time.
In recent years, there are few researches on the optimization of HFSP based on the surrogate subgradient method For different production scheduling problems, it is necessary to study the specific implementation of the algorithm to obtain a satisfactory solution. Therefore, aiming at the total weighted completion time, this paper investigates the effectiveness of solving the embedded interleaved subgradient method LR of HFSP with waiting consideration, extending the theory of LR algorithm and its application.
Mathematical description
The HFSP studied in this paper is to schedule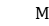 
workpieces in the same machining order on G-stage parallel machines, with the goal of minimizing the total weighted completion time to reduce inventory. The waiting time of the workpiece between adjacent processing stages is not allowed to exceed the upper limit of waiting. Assuming that each operation is not allowed to be interrupted, each workpiece can only start processing at time 
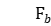, and the transportation time cannot be ignored.
Symbol description
Known parameters: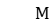 
is the total number of workpieces; 
is the total number of stages;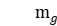 
is the number of machines available for stage 
; 
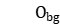is the workpiece 
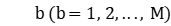in stage
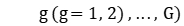processing time; 
is the release time of workpiece 
; 
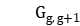is the transportation time of stages 
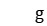and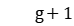 
; 
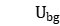is the upper waiting limit between adjacent stages 
and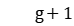 
of workpiece 
; 
is the total planned time level.
Decision variable: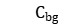 
is the completion time of workpiece
in stage 
; 
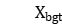is a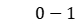 
variable, if workpiece 
is being processed in stage 
at time 
, its value is 1, otherwise it is 0.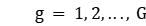 
; 
; 
.
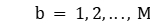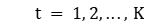Integer programming model
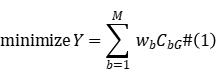
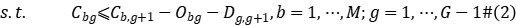
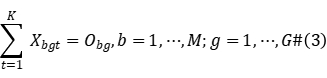
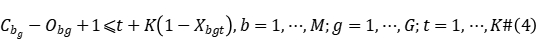
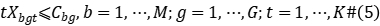
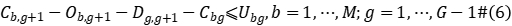
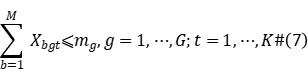
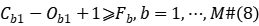
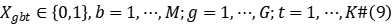
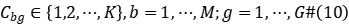
Constraint (2) represents the operation priority of a workpiece between processing stages; constraints (3) to (5) define the time interval that each workpiece occupies the machine in the processing stage; constraint (6) represents the waiting time after the workpiece is machined at stage 
and delivered to stage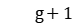 
cannot exceed the upper limit of waiting; Constraint (7) states that all machine requirements must meet the number of machines available at that time; Constraint (8) states that each workpiece can only be Processing can only be started at the start end of the production system; constraints (9) to (10) define the value range of variables.
Solution method
Based on the workpiece decomposition strategy, the machine capability constraints are relaxed into the objective function by introducing Lagrangian multipliers. The purpose of the relaxation capability constraints is to decompose the relaxed problem into multiple workpiece-level sub-problems that are relatively easy to solve.
Relaxation and decomposition
The Lagrangian multiplier vector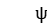 
(whose component is is introduced, and the constraint (7) is relaxed into the objective function to form the Lagrangian relaxation problem:
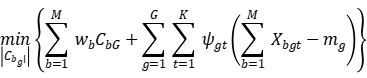
Satisfy constraints (2)～(6), (8)～(10) and:
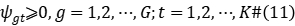
Then the Lagrange duality problem is:
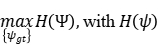
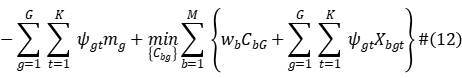
Satisfy constraints (2)～(6), (8)～(11).
Given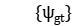 
, the artifact-level subproblem 
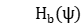of artifact 
is:
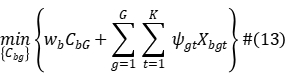
Satisfy constraints (2)～(6), (8)～(11).
Decomposition and coordination
Figure 1 shows the two-level decomposition-coordination structure of the LR algorithm. At "low level", M artifact-level subproblems are solved given the multipliers 
are known; at "high level", the multipliers 
are updated based on the degree of constraint violation, and then design a heuristic based on the solution of the subproblem to transform it into a feasible solution until the end of the iterative process[4].
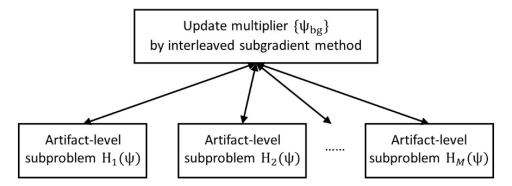
Figure 1 Two-level decomposition-coordination structure
The difference between the designed LR algorithm and the traditional LR algorithm is that the designed algorithm approximately solves the subproblems in each iteration and uses the interleaved subgradient method[5] to update the multipliers in the "advanced".
Approximate solution of subproblems
Given a certain workpiece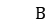 
and the multiplier 
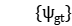, the recursive relation for optimal solution of backward dynamic programming is:
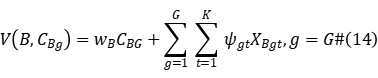
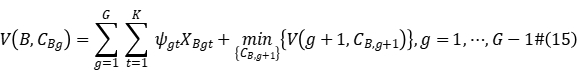
Then trace forward to get the optimal solution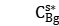 
of the sub-problem in the s-th iteration.
When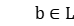 
and 
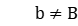, let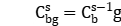 
; when 
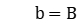let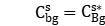 
, then obtain an approximate solution to the relaxation problem.
Construction of feasible solutions
Based on the solution of the relaxation problem obtained above, for each stage 
, arrange the workpieces in increasing order of the start time of the stage, and then assign them to the available machines in turn. If the waiting time between adjacent processing stages exceeds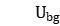 
, then delay the start time of the workpiece in phase 
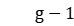until the waiting time constraint is satisfied.
Dual problem
The traditional subgradient method requires the optimal solution of all Lagrangian problems in each iteration to obtain the subgradient direction, so when the scale of the problem is large, the solution of the relaxation problem is complicated and time-consuming. To this end, the interleaved subgradient method[5] is designed to reduce the solution time spent in each iteration, and it can update the multipliers after each sub-problem is solved.
The surrogate dual function is defined as:
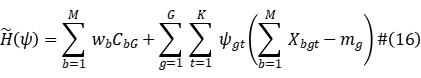
Then the surrogate subgradient is defined as:
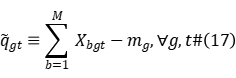
The execution process of the interleaved subgradient method is as follows:
Step 0 initializes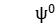 
and minimizes all subproblems to get 
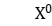, that is:
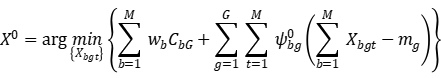
Calculate the dual cost and subgradient, update the multipliers along the direction of the subgradient. Let the subproblem label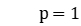
.
Step 1 Knowing the 
of the s-th iteration, optimally solve the p-th sub-problem while keeping the solutions of other sub-problems unchanged, and calculate the surrogate dual cost and surrogate subgradient according to equations (16) and (17).
Step 2 Update the Lagrange multipliers from the 
and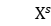 
obtained in the previous step:
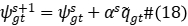
where the step size 
is defined as:
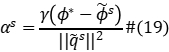
Here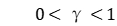 
, 
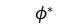is the estimated value of the optimal dual cost, and 
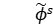is the surrogate dual cost of the s-th iteration.
Step 3 Let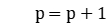 
, if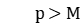 
, then reset 
.
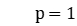Step 4 If the CPU time reaches a certain limit or the agent dual gap is less than a small number, the program stops, otherwise it returns to Step 1.
Simulation results
Using C language to execute the designed algorithm on PC (2.10GHz CPU), the simulation experiment compares the algorithm with the traditional LR based on subgradient method. First, tests on small and medium scale problems demonstrate the effectiveness of the two algorithms; then the results of running on real large scale problems are compared to estimate the performance on real scale problems.
The maximum size of the tested problem is 200 artifacts, 4 stages, 5 parallel machines. For each set of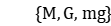 
, 10 instances are randomly generated; in each instance, the data of each workpiece is randomly generated as follows: the weight and processing time satisfy the uniform distribution 
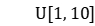, and the release time satisfies the uniform distribution 
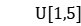. The transportation time between adjacent processing stages satisfies the uniform distribution 
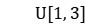. The waiting time is taken as 5, 15. The total time level is set as the sum of all machining times. The algorithm terminates after 90 seconds.
LR-ISG is used to represent the LR based on the interleaved subgradient method, and LR-SG is used to represent the traditional LR based on the sub-gradient method. The performance indicators of the two algorithms are measured by the duality gap and the number of iterations. SDG is defined as the surrogate dual gap (%), and its value is equal to (UB-SLB)/SLB×100%, DG is the true dual gap, calculated by (UB-LB)/LB×100%, IN represents the number of iterations, here , UB represents the feasible cost, that is, the upper bound of the original problem; LB represents the dual cost, that is, the lower bound; SLB is the agent dual cost.
Example 1
In this section, the cases of 40 and 80 workpieces are tested, and the calculation results are shown in Tables 1-2. The results in the table (except the last row) are the average of 10 groups of instances of the same scale. From the table it can be seen that:
For the case of 40 workpieces, when
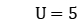and 15, the average dual clearances obtained by LR-ISG are 2.64% and 3.09%, respectively, and those obtained by LR-SG are 2.97% and 2.97%, respectively. Therefore, the proposed algorithm reduces the dual gap by 0.33% and 0.17% on average compared with the traditional LR.For the case of 80 workpieces, when
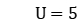and 15, the average dual gaps obtained by LR-ISG are 5.22% and 6.04%, respectively, and those obtained by LR-SG are 5.46% and 5.46%, respectively. Therefore, the proposed algorithm reduces the dual gap by 0.24% and 1.95% on average compared with the traditional LR.In the same calculation time, the number of iterations performed by LR-ISG is dozens of times that of LR-SG. This is because LR-ISG only optimally solves one sub-problem in each iteration. It's time is much less than solving all subproblems.
When
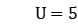and 15, the deviations of LR-ISG's surrogate dual gap and true dual gap are 0.04% and 0.05% (for 40 workpieces), 0.38% and 0.49, respectively % (for 80 workpieces), that is, the surrogate dual gap obtained by LR-ISG is not much different from the real dual gap.
To sum up, for small and medium-sized problems, these two algorithms can obtain a good near-optimal solution in a short computing time (90s), and the proposed LR algorithm performs better.
Table1 Test results when M=40
| G×mg | U = 5 | U = 15 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LR-ISG | LR-SG | LR-ISG | LR-SG | |||||||
| SDG | DG | IN | DG | IN | SDG | DG | IN | DG | IN | |
| 3×3 | 2.37 | 2.43 | 32873 | 3.18 | 1513 | 2.53 | 2.60 | 20815 | 3.42 | 657 |
| 3×4 | 2.02 | 2.05 | 33625 | 2.44 | 1551 | 2.42 | 2.46 | 21144 | 2.84 | 681 |
| 3×5 | 1.66 | 1.68 | 33801 | 1.75 | 1601 | 1.92 | 1.92 | 22164 | 1.81 | 728 |
| 4×3 | 4.23 | 4.33 | 19792 | 5.24 | 852 | 4.69 | 4.83 | 11703 | 5.67 | 360 |
| 4×4 | 2.67 | 2.69 | 21706 | 2.94 | 842 | 3.32 | 3.34 | 11498 | 3.08 | 362 |
| 4×5 | 2.67 | 2.68 | 21228 | 2.24 | 843 | 3.34 | 3.36 | 11311 | 2.74 | 348 |
| avg | 2.60 | 2.64 | 27171 | 2.97 | 1200 | 3.04 | 3.09 | 16439 | 3.26 | 523 |
Table2 Test results when M=80
| G×mg | U = 5 | U = 15 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LR-ISG | LR-SG | LR-ISG | LR-SG | |||||||
| SDG | DG | IN | DG | IN | SDG | DG | IN | DG | IN | |
| 3×3 | 3.84 | 4.44 | 12488 | 5.24 | 412 | 4.67 | 5.54 | 9221 | 6.75 | 173 |
| 3×4 | 3.79 | 4.02 | 12964 | 4.19 | 409 | 4.29 | 4.60 | 8800 | 5.66 | 171 |
| 3×5 | 3.60 | 3.71 | 13318 | 3.56 | 400 | 4.18 | 4.30 | 7810 | 4.96 | 170 |
| 4×3 | 6.41 | 7.30 | 7438 | 7.76 | 216 | 6.93 | 7.98 | 5184 | 11.24 | 91 |
| 4×4 | 6.19 | 6.53 | 7859 | 6.68 | 213 | 7.13 | 7.59 | 5081 | 10.42 | 90 |
| 4×5 | 5.22 | 5.31 | 8296 | 5.32 | 215 | 6.07 | 6.21 | 5180 | 8.90 | 91 |
| avg | 4.84 | 5.22 | 10394 | 5.46 | 311 | 5.55 | 6.04 | 6879 | 7.99 | 131 |
Example 2
The number of workpieces tested in this section is taken from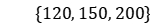 
, and the test results are shown in Tables 3 to 5. From the results in the table, the following conclusions can be drawn:
When
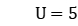, for the cases of 120 workpieces, 150 workpieces and 200 workpieces, the average surrogate-dual gap obtained by LR-ISG at 5492, 3732 and 1939 iterations, respectively, is 5. 44%, 5. 25%, 5. 34%; the real dual gaps are 6. 49%, 6. 70%, 7. 83%. The dual gap obtained by LR-SG at 140, 90 and 51 iterations, respectively, is 8. 20%, 10. 86%, 18. 79%. Therefore, the dual gap of LR-ISG is lower than that of LR-SG by 1. 71%, 4. 16%, 10. 96%.When
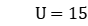, for the cases of 120 workpieces, 150 workpieces and 200 workpieces, the average surrogate duality gap obtained by LR-ISG at 4130, 2900 and 1860 iterations, respectively, is 6. 94%, 7. 32%, 8. 63%; the real dual gaps are 8. 49%, 9. 60%, 13. 56%. The dual gaps obtained by LR-SG at 59, 36 and 18 iterations, respectively, are 16. 54%, 27. 42%, 51. 97%. Therefore, the dual gap of LR-ISG is lower than that of LR-SG 8. 05%, 17. 82%, 38. 41%.When
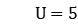and 15, the deviations of LR-ISG's surrogate dual gap and true dual gap are 1.05% and 1.55% (for 120 workpieces), 1.45% and 2.28%, respectively (for 150 workpieces), 2.49% and 4.93% (for 200 workpieces), that is, as the scale of the problem increases, the difference between the surrogate dual gap and the true dual gap obtained by LR-ISG is also greater.
To sum up, LR-ISG can obtain a good near-optimal solution for large-scale problems in a short computing time (90s), and LR-ISG is significantly better than LR-SG in terms of solution quality and computational efficiency.
Table3 Test results when M=120
| G×mg | U = 5 | U = 15 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LR-ISG | LR-SG | LR-ISG | LR-SG | |||||||
| SDG | DG | IN | DG | IN | SDG | DG | IN | DG | IN | |
| 3×3 | 2.81 | 3.79 | 6782 | 5.36 | 186 | 5.58 | 8.01 | 5678 | 12.93 | 77 |
| 3×4 | 3.88 | 4.73 | 7302 | 5.80 | 184 | 5.57 | 6.80 | 5364 | 11.00 | 79 |
| 3×5 | 4.66 | 5.14 | 7601 | 5.85 | 183 | 5.64 | 6.43 | 5405 | 10.75 | 76 |
| 4×3 | 6.91 | 9.91 | 3435 | 11.81 | 92 | 8.33 | 11.04 | 2650 | 23.31 | 38 |
| 4×4 | 7.01 | 8.07 | 3784 | 10.72 | 96 | 8.09 | 9.43 | 2839 | 21.16 | 40 |
| 4×5 | 7.36 | 8.02 | 4046 | 9.64 | 98 | 8.40 | 9.25 | 2844 | 20.11 | 40 |
| avg | 5.44 | 6.49 | 5492 | 8.20 | 140 | 6.94 | 8.49 | 4130 | 16.54 | 59 |
Table4 Test results when M=150
| G×mg | U = 5 | U = 15 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LR-ISG | LR-SG | LR-ISG | LR-SG | |||||||
| SDG | DG | IN | DG | IN | SDG | DG | IN | DG | IN | |
| 3×3 | 1.93 | 2.89 | 4415 | 5.65 | 119 | 5.21 | 8.11 | 3625 | 19.73 | 49 |
| 3×4 | 3.88 | 4.98 | 4954 | 7.38 | 116 | 5.57 | 7.48 | 3768 | 16.89 | 50 |
| 3×5 | 4.40 | 5.23 | 5249 | 7.30 | 118 | 6.15 | 7.45 | 3832 | 17.15 | 49 |
| 4×3 | 6.55 | 9.29 | 2451 | 15.36 | 63 | 9.15 | 13.09 | 1955 | 36.97 | 25 |
| 4×4 | 7.28 | 9.16 | 2550 | 14.93 | 63 | 8.99 | 11.25 | 2062 | 37.20 | 23 |
| 4×5 | 7.48 | 8.62 | 2771 | 14.53 | 62 | 8.86 | 10.22 | 2157 | 36.60 | 22 |
| avg | 5.25 | 6.70 | 3732 | 10.86 | 90 | 7.32 | 9.60 | 2900 | 27.42 | 36 |
Table5 Test results when M=200
| G×mg | U = 5 | U = 15 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LR-ISG | LR-SG | LR-ISG | LR-SG | |||||||
| SDG | DG | IN | DG | IN | SDG | DG | IN | DG | IN | |
| 3×3 | 1.64 | 2.85 | 2447 | 11.36 | 67 | 5.91 | 10.87 | 2290 | 41.16 | 24 |
| 3×4 | 2.81 | 4.35 | 2387 | 11.14 | 67 | 5.84 | 8.91 | 2452 | 36.47 | 24 |
| 3×5 | 4.75 | 6.38 | 2620 | 12.00 | 67 | 6.23 | 8.43 | 2545 | 35.03 | 25 |
| 4×3 | 5.75 | 10.09 | 1291 | 26.53 | 34 | 10.89 | 20.29 | 1205 | 74.86 | 12 |
| 4×4 | 7.69 | 11.21 | 1395 | 25.58 | 35 | 10.98 | 16.54 | 1316 | 63.97 | 13 |
| 4×5 | 9.37 | 12.10 | 1496 | 26.14 | 36 | 11.91 | 16.34 | 1350 | 60.35 | 13 |
| avg | 5.34 | 7.83 | 1939 | 18.79 | 51 | 8.63 | 13.56 | 1860 | 51.97 | 18 |
Summary
In this paper, an improved LR algorithm with embedded interleaved subgradient method is designed for HFSP considering waiting, and the goal is to minimize the total weighted completion time. The computational complexity and required computation time of each iteration are simplified by the approximate solution of the relaxation problem, and a reasonable asynchronous subgradient direction is obtained to search for a better solution. The simulation results show that the proposed algorithm can obtain a good near-optimal solution in a short computing time when solving small to large-scale problems, especially for practical large-scale problems, its performance is significantly better than that of traditional LR. Further work can generalize the method to complex production scheduling problems with other production characteristics.
References:
[1] Gicquel C，Hege L，Minoux M，van Canneyt W． A discrete time exact solution approach for a complex hybrid flow-shop scheduling problem with limited constraints[J]． Computers＆ OperationsＲesearch，2012，39(3) : 629-636．
[2] Niu Q，Zhou T，Fei M，Wang B． An efficient quantum immune algorithm to minimize mean flow time for hybrid flow shop problems[J]． Mathematics and Computers in Simulation，2012，84: 1-25．
[3] Gupta J N D． Two-stage hybrid flowhsop scheduling problem[J]． Journal of the OperationalＲesearch Society，1988，39: 359-364．
[4] Chen H X，Luh P B． An alternative framework to Lagrangian relaxation approach for job shop scheduling[J］． European Journal of OperationalＲesearch，2003，149(3) : 499-512．
[5] Zhao X，Luh P B，Wang J． Surrogate gradient algorithm for lagrangian relaxation[J]． Journal of Optimization Theory and Application，1999，100(3) : 699-712．
